올림피우스는 결승점의 절반을 가고, 그 나머지 절반의 절반을 가고, 또 그 절반을 가고… 더보기
데이터를 빠르게 반으로 갈라버리는 퀵 정렬을 배워보자. 부제목에 쓰인 이야기는 제논의 역설 중 하나이다. ‘아킬레우스와 거북이의 경주’도 있는데 재밌으니 한번 찾아보자.
- 알아야 할 것
0. 재귀 → 백트래킹
1. 분할 정복
2. 퀵 정렬
1. 분할 정복
요약 : 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이나 알고리즘이다. (출처 위키백과)
어려운 문제를 풀어야 할 때, 그 문제와 같은 형식으로 아주 쉬운 문제를 만들어 먼저 해결 방법을 익히고 어려운 문제를 풀어본 적이 있는가? 내가 어릴 때 읽었던 수학 소설책에서 나왔던 방법이다. 제목이 <피타고라스 구출작전>이었나? 같은 시리즈의 책도 한 권 더 있었는데 정확히 어느 쪽에서 나온 얘기인지는 기억나지 않는다. 그래도 어릴 때부터 지금까지 내가 잊지 않고 문제가 막히면 한번씩은 생각해보는 좋은 방법이다. 분할 정복은 이 방법과 비슷하다. 큰 문제 하나를 작은 문제 여러 개로 만들어 각각 해결한 다음 하나의 큰 답으로 만들어낸다.
2. 퀵 정렬
제논의 역설에서 올림피우스는 결승점에 도달하지 못했을지도 모르지만 퀵 정렬은 결승점에 도달할 수 있는 알고리즘이다. 그 과정을 설명하자면 다음과 같다.
- 여기 크기가 아주 크고 다양한 값이 뒤섞인 배열이 있다. 이 배열을 빠르게 정리하고 싶다. 우선 배열 내에서 기준이 될 값(pivot 피벗이라고 한다)을 하나 정한다.
- 배열의 처음과 끝에서부터 하나씩 좁혀오며 기준 값과 크기를 비교한다. 처음에서부터 오는 값을 i, 끝에서부터 오는 값을 j라고 하자. i가 기준 값보다 크고, j가 기준 값보다 작을 때 두 값을 뒤바꾼다. 이 과정을 i가 j보다 뒤에 있게 될 때까지 계속한다. i와 j는 대칭되게 이동하지 않을 수 있다.
- i가 j보다 뒤로 갔다면 전체 배열을 반으로 나눈다. 반으로 나눈 두 배열을 arr1, arr2라고 하자. arr1과 arr2에서 각각 기준 값을 정하고 2번의 과정을 반복한다. 끝나면 두 배열을 다시 각각 반으로 나눈다.
- 반으로 나누어진 배열의 크기가 1이 될 때까지 2번과 3번을 반복한다. 크기가 1인 배열은 항상 정렬되어 있는 것과 같으므로 그 때 정렬이 끝난다.
글만 보면 아쉽기도 하고, 위키백과에 좋은 이미지가 있어서 가져왔다. 다만 기준 값을 고르는 위치가 내가 뒤에 설명할 예시 코드와는 다르다는 점은 알아둬야 한다. 내 코드는 배열의 중간에 있는 값을 피벗으로 정한다. 이미지는 이해를 돕는 참고용으로만 보자!
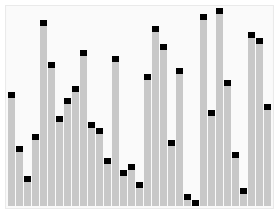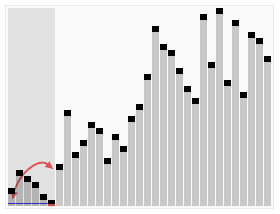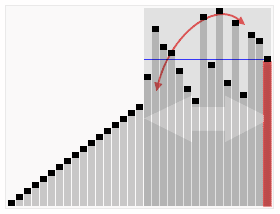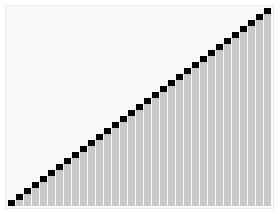
3. 그래서 이걸 코드로 어떻게 쓰는데요
이번에도 직접 코드를 써볼 수 있을까 해서 해봤는데 영 신통치 않았다.. 그래서 다른 예시 참고해서 고쳐왔다. 참고한 블로그는 이쪽 : https://dpdpwl.tistory.com/46
깃허브 : [C++/퀵 정렬 예시 코드.cpp], [파이썬/퀵 정렬 예시 코드.py]
[C++ 예시 코드]
부연설명 : swap 함수를 사용하지 않을 생각이라면 <algorithm> 클래스는 가져오지 않고, swap 없이 임시 변수를 하나 더 두어 서로 자리를 바꾸어도 된다. 프로그래머 두 명이 자리를 바꾸려면 의자 세 개가 필요하다는 말 처럼.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <algorithm> // swap 함수를 사용하기 위함
using namespace std;
// 퀵 정렬 함수
void qsort(int list[], int i, int j);
int main()
{
int s = 12; // 배열 크기
int ar[] = { 5, 9, 6, 9, 2, 9, 1, 3, 7, 10, 4, 8 }; // 정렬할 배열
qsort(ar, 0, s - 1); // 정렬 함수 호출
for (int i = 0; i < s; i++) // 정렬한 배열 출력
cout << ar[i] << " ";
return 0;
}
// 퀵 정렬 함수
void qsort(int list[], int i, int j) // 배열은 기본적으로 참조 전달이기 때문에 &를 붙이면 안 된다
{
int p = (i + j) / 2; // 기준 값 피벗
int ni = i; // 다음 호출에 쓸 i
int nj = j; // 다음 호출에 쓸 j
if (i >= j) // 배열 크기가 1이라면 정렬 끝, 리턴
return;
while (i < j) { // i와 j가 만나면 중단
while (list[i] < list[p]) // i 쪽에서 기준 값보다 큰 값 찾기
i++;
while (list[j] > list[p]) // j 쪽에서 기준 값보다 작은 값 찾기
j--;
if (i <= j) { // i가 왼쪽에 있고 j가 오른쪽에 있을 때에만 실행, 겹쳐도 된다.
swap(list[i], list[j]); // i와 j 자리에 있는 두 요소를 서로 바꿈
// 사용한 i와 j를 바꿔주지 않으면 무한루프가 생김
i++;
j--;
}
}
// 나누어진 배열 양쪽에 대한 재귀 호출
qsort(list, ni, j);
qsort(list, i, nj);
}
[파이썬 소스 코드]
참고 : 파이썬은 프로그래머 두 명이 의자 두 개만으로도 자리를 바꿀 수 있는 언어이기 때문에 굳이 swap 함수 같은 것이 필요하지 않다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 퀵 정렬 함수
def qsort(lis, i, j):
p = (i + j) // 2 # 기준 값 피벗
next_i = i # 다음 호출에 쓸 i
next_j = j # 다음 호출에 쓸 j
if i >= j: # 배열 크기가 1이라면 정렬 끝, 리턴
return
while i < j: # i와 j가 만나면 중단
while lis[i] < lis[p]: # i 쪽에서 기준 값보다 큰 값 찾기
i += 1
while lis[j] > lis[p]: # j 쪽에서 기준 값보다 작은 값 찾기
j -= 1
if i <= j: # i가 왼쪽에 있고 j가 오른쪽에 있을 때에만 실행, 겹쳐도 된다.
lis[i], lis[j] = lis[j], lis[i] # i와 j 자리에 있는 두 요소를 서로 바꿈
# 사용한 i와 j를 바꿔주지 않으면 무한루프가 생김
i += 1
j -= 1
# 나누어진 배열 양쪽에 대한 재귀 호출
qsort(lis, next_i, j)
qsort(lis, i, next_j)
ar = [5, 9, 6, 9, 2, 9, 1, 3, 7, 10, 4, 8] # 정렬할 배열
s = len(ar) # 배열 크기
qsort(ar, 0, s - 1) # 정렬 함수 호출
print(ar) # 정렬한 배열 출력
