홈 [자료구조] 그래프와 다익스트라
포스트
취소

[자료구조] 그래프와 다익스트라

게시 2022-11-26
By dapin1490
22 분읽는 시간

할 일

[과제]
이번 숙제는 다음 내용을 포함합니다.
1. 그래프 표현 방법(코드 중심)으로 설명합니다. (O)
2. 다익스트라 알고리즘을 설명하고, 코드를 구현합니다. (O)
3. (옵션) 백준 알고리즘 다음 문제를 풀어봅니다. (X)
- 1753 최단경로 : 시간초과
- 1238 파티
- 1504 특정 최단 경로
- 1177 최소비용 구하기
4. (옵션) BFS 관련 문제를 풀어 봅니다. (X)

[메모]
다익스트라 알고리즘은 이 알고리즘을 수행하는 그래프가 연결 그래프일 것을 전제하나?
: 그럴 것 같긴 한데. 기본적으로 한 정점에서 다른 모든 정점으로 가는 경로가 있음을 전제하고 있다. 그래프가 연결되지 않아 경로가 없는 경우를 고려하지 않는다.
추가) 연결되지 않은 경우는 거리를 무한으로 냅두면 된다.

목차

  1. 그래프 구현하기
  2. 다익스트라

그래프 구현하기

그래프에 대한 이론적인 설명은 여기에서 볼 수 있다. 이 글에서는 가중치 그래프를 중점으로 다룬다.

가중치 그래프는 정점과 간선, 가중치로 구성된다. 이 구성 요소는 그래프를 코드로 구현할 때에도 거의 같다. 각각의 정점이 어떠한 정보를 가져야 한다면 정점을 중심으로 구조체를 구상하면 되고, 정점이 특별한 정보를 갖지 않는다면 간선을 중심으로 구조체를 만드는 방법도 있다. 지난 글인 [자료구조] BFS와 DFS에서는 각 정점이 특정 station으로부터의 거리 값을 갖도록 했기 때문에 정점을 중심으로 구조체를 만들었다. 이번에는 정점이 아무런 정보도 갖지 않는다는 전제로 간선을 중심으로 그래프를 구현하고자 한다.

가장 기본 단위가 될 간선 구조체부터 생각해 보자. 무방향 그래프와 방향 그래프의 간선 구조체를 따로 만들기보다는, 기본 단위인 만큼 두 그래프에 모두 사용할 수 있도록 방향이 있는 간선을 만드는 게 좋을 것 같다. 방향 그래프에는 그대로 사용할 수 있고, 무방향 그래프를 만들 때는 서로 반대 방향의 간선 2개를 한번에 추가하면 된다. 따라서 이 구조체가 가져야 할 정보는 시작점과 종점, 가중치이다.

시작점과 종점, 다시 말해 각 정점은 간단하게 양수인 정수형의 ID로 구분한다고 하자. 가중치는 지금까지 정수로 사용해오긴 했지만, 때에 따라 실수를 사용하고 싶을 수도 있을 것이다. 혹은 사용자가 정의한 새로운 자료형을 사용할 수도 있다. 이럴 때 필요한 것이 템플릿이다(템플릿에 대해 새로 배웠기 때문에 같이 활용할 목적일 뿐이다). 정리하자면 방향이 있는 간선 구조체를 만들고, 간선의 시작점과 종점은 unsigned int로, 가중치는 템플릿으로 만들 것이다.

아래는 간선 구조체 코드이다.

1
2
3
4
5
6

template <typename T>
struct Edge {
    T w; // 가중치
    unsigned from; // 시작점
    unsigned to; // 종점
};

다음은 저 간선을 이용한 그래프를 만들어야 한다. 그래프는 간선의 모임으로 만들어지며, 몇 가지 연산이 필요하다. 지금은 아주 기본적인 연산만 만들 것이다. 방향이 있는 간선과 방향이 없는 간선을 추가하는 연산이다. 위에서 만든 간선 구조체에 템플릿이 사용되었기 때문에 그래프 클래스도 템플릿을 사용해야 한다.

간선 구조체가 방향이 있기 때문에 그래프에 방향이 있는 간선을 추가하는 연산은 1개의 간선 구조체를 추가하면 되고, 방향이 없는 간선을 추가할 때는 서로 반대 방향의 간선 2개를 추가하면 된다.

그래프 클래스 코드는 아래에 있다. 교수님의 코드를 참고하여 작성했다.

코드를 보기에 앞서 유의할 점은 이 그래프 클래스는 정점의 수가 제한되어 있다는 것이다. 처음부터 정점의 총 개수를 알고 그리는 그래프이다. TGraph::print()에서 정점마다 연결된 다른 정점을 출력하는 반복문을 실행하기 위해 정점의 개수를 알고 있어야 한다. 그리고 모르는 정점이 추가되지 않도록 하기 위해 간선을 추가하는 연산에서 정점의 ID를 확인한다.

사실 이 그래프 클래스는 이후에 다익스트라 알고리즘에 사용하는 것이 목적이기 때문에 그래프를 구성하는 모든 정점이 최소 하나 이상의 간선으로 연결되어 있을 것을 전제한다. 그런 의미에서도 정점의 수를 제한하는 것으로 보인다. 다익스트라 알고리즘을 사용하지 않고 그래프라는 개념 자체를 구현하고자 한다면 정점의 수가 아니라 정점의 ID 최댓값을 저장하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

enum class _error : int { shut_down, ValueErrorInt, ValueErrorChar, UnknownError };

// C++ 에러 메시지 참고 : https://learn.microsoft.com/ko-kr/cpp/error-messages/compiler-errors-1/c-cpp-build-errors?view=msvc-170
void error(_error code, string message="") {
    if (!message.empty())
        cout << "error: " << message << "\n";

    switch (code) {
    case _error::shut_down:
        cout << "프로그램 비정상 종료\n";
        break;
    case _error::ValueErrorInt: // 잘못된 입력 - int
        cout << "ValueErrorInt: int 값이 입력되어야 합니다.\n";
        break;
    case _error::ValueErrorChar: // 잘못된 입력 - char
        cout << "ValueErrorChar: char 값이 입력되어야 합니다.\n";
        break;
    default:
        cout << "UnknownError: 알 수 없는 오류\n";
    }

    exit(1); // 프로그램 비정상 종료
}

template <typename T>
class TGraph {
private:
    unsigned v; // 정점 수
    vector<Edge<T>> edges; // 그래프가 갖는 간선들

public:
    // 생성자
    TGraph() { this->v = 0; }
    TGraph(unsigned v) { this->v = v; }

    // 함수 정의에 쓰인 const : 이 함수 안에서 쓰는 값들을 변경할 수 없다
    unsigned size() const { return v; } // 그래프가 갖는 정점의 수를 반환
    auto& edges_from() const { return this->edges; } // 그래프가 갖는 간선들을 반환
    // 특정 정점에 연결된 간선들만 반환
    auto edges_from(unsigned i) const { // 여기에 & 쓰면 결과가 제대로 반환이 안 됨. 근데 이유는 모름..
        vector<Edge<T>> edge_from_i;
        for (auto& e : edges) {
            if (e.from == i)
                edge_from_i.push_back(e);
        }
        /*for (int idx = 0; idx < this->edges.size(); idx++) {
            if (this->edges[idx].from == i)
                edge_from_i.push_back(edges[idx]);
        }*/
        return edge_from_i;
    }

    void add(Edge<T>&& e) { // 방향 간선 추가
        if (e.from > 0 && e.from <= this->v && e.to > 0 && e.to <= this->v)
            this->edges.push_back(e);
        else
            error(_error::shut_down, "정점 범위 초과");

        return;
    }

    void add_undir(Edge<T>&& e) { // 무방향 간선 추가
        if (e.from > 0 && e.from <= this->v && e.to > 0 && e.to <= this->v) {
            this->edges.push_back(e);
            this->edges.push_back(Edge<T>{e.w, e.to, e.from});
        }
        else
            error(_error::shut_down, "정점 범위 초과");

        return;
    }

    void print() { // 그래프 출력
        for (int i = 1; i <= v; i++) {
            cout << "# " << i << " : ";
            vector<Edge<T>> edge = this->TGraph::edges_from(i);
            for (auto& e : edge)
                cout << "(" << e.to << ", " << e.w << ")  ";
            cout << "\n";
        }
        return;
    }
};

다익스트라

다익스트라 알고리즘은 주어진 연결 그래프에서 최단경로를 찾는 것이 목적인 알고리즘이다. 하나의 시작점을 기준으로 하며, 그 점으로부터 다른 모든 점까지 도달하는 비용의 최솟값을 구한다. 시작점에서 가장 가까운 곳부터 시작해 정점을 하나씩 방문하며 알아낸 비용의 최솟값을 이용해 또다른 정점으로의 최소 비용을 알아내는 방식이다. 모든 경로에는 사이클이 없어야 한다지만 자동으로 사이클이 생기지 않는 경로를 찾게 되니 굳이 검사할 필요는 없다.

다시 한 번 자세히 알고리즘 수행 과정을 보자.
필요한 것은 시작점과 시작점으로부터의 거리를 저장할 선형 자료구조(배열, 벡터 등 종류 상관 없음)이다.

  1. 시작점을 방문하여 시작한다. 시작점에서 나머지 모든 정점까지의 거리를 계산하되, 간선이 직접 연결된 경우에만 거리를 계산하고, 간선이 직접 연결되지 않은 정점은 거리를 무한으로 간주한다.
  2. 계산된 거리 중(무한 포함)에서, 그리고 아직 방문하지 않은 정점 중에서 가장 가까운 곳으로 이동한다.
  3. 해당 정점에서 다시 거리를 계산해야 한다. 지금 방문한 정점에서 갈 수 있는 모든 정점에 대해, 앞서 1번에서 계산했던 값과, 지금 방문한 정점을 거쳐 그곳으로 가는 거리를 비교해 더 작은 쪽으로 업데이트한다.
  4. 업데이트된 거리 중에서, 그리고 아직 방문하지 않은 정점 중에서 가장 가까운 곳으로 이동한다.
  5. 이후 모든 정점을 방문할 때까지 3번과 4번을 반복한다.
  • 일반화 : n번째 방문한 정점에서 갈 수 있는 다른 모든 정점에 대해, n-1번째 방문한 정점에서 계산한 거리와 현재 정점에서 해당 정점으로 가는 거리를 비교하여 더 작은 쪽을 적용한다. 시작점에서 시작할 때는(n=1) n-1번째 정점이 없으므로 모든 거리를 무한으로 간주한다.

나는 세 가지 다익스트라 함수를 만들었다. 첫 번째는 시작점으로부터 목적지까지 최소 비용만을 계산하고, 두 번째는 첫 번째의 결과에 더해 해당 경로로 가기 위해 직전에 방문해야 할 정점을 같이 구하고, 세 번째는 두 번째에서 구한 정보들을 이용해 시작점부터 모든 정점으로의 완전한 경로를 구한다. 함수의 이름은 각각 dijkstra, dijkstra_path, dijkstra_fullpath이다. 전체 코드는 깃허브에서 볼 수 있다.

그러나 내가 쓴 다익스트라 코드는 한 가지 과정에서 상당히 비효율적으로 동작한다. 다음에 방문할 정점을 고르기 위해서는 거리가 가장 짧으면서 아직 방문하지 않은 정점을 찾아야 하는데, 이 과정을 매번 우선순위 큐에 모든 간선을 넣었다 빼면서 수행하고 있다. 아래 있는 예제는 간단하기 때문에 이런 코드로도 금방 답이 나오지만 데이터의 양이 조금만 커져도 내 코드는 결과를 내기까지 상당히 오랜 시간이 걸릴 것이다. 사실 이 문제는 힙을 좀 더 섬세하게 다루면 금방 해결된다. 이번엔 내가 시간이 부족하고, 이해도 부족해서 그러지 못했을 뿐이다. 요점은 이 코드에는 결함이 있음을 감안하고 봐달라는 말이다.

결함이 있긴 하지만, 남이 쓴 코드를 이해하는 좋은 방법 중 하나는 예시를 보는 것이다. 그래서 예시 그래프도 준비했다.

22.12.04 수정
다익스트라 함수에 사용된 우선순위 큐의 사용 방법을 약간 바꿨다. 여전히 백준 문제는 통과되지 않는 것을 봐선 어딘가 더 효율적으로 쓸 수 있는 방법이 있는 모양이지만 지금 내가 이해한 선에서 쓸 수 있는 만큼 썼다.

[이미지 1] 다익스트라 예시 그래프

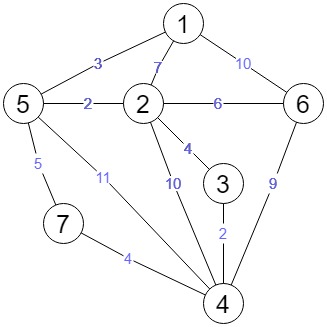
위 그래프를 이용하여 세 가지 다익스트라 함수를 실행한 결과는 이 링크에서 볼 수 있다.

코드의 길이가 길어 여기에 모든 코드를 올리지는 않고, 내가 구현한 다익스트라 함수의 모든 기능을 포함하는 dijkstra_fullpath 함수만 올리겠다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

struct cmp { // 다익스트라 우선순위 큐 비교 연산자 : 가중치가 적고 정점 번호가 적은 것을 우선으로 함
    bool operator()(pair<unsigned, unsigned> a, pair<unsigned, unsigned> b) {
        if (a.second == b.second)
            return a.first >= b.first;
        else
            return a.second > b.second;
    }
};

// 응용 : 다익스트라 경로 탐색 - 모든 경로 표시
vector<pair<unsigned, list<unsigned>>> dijkstra_fullpath(unsigned s) { // s는 시작점
    vector<pair<unsigned, unsigned>> d(v + 1, make_pair(numeric_limits<unsigned>::max(), s)); // 저장용 거리 벡터. 정점 번호가 1부터 시작함. (최소 비용 거리, 직전 경로 정점)
    vector<bool> visited(v + 1, false); // 방문 여부 초기화
    priority_queue<pair<unsigned, unsigned>, vector<pair<unsigned, unsigned>>, cmp> next_visit; // 다음에 방문할 정점 : (정점, 거리)
    vector<pair<unsigned, list<unsigned>>> full_path(v + 1); // 모든 경로 표시 벡터 : (거리, 경로)

    unsigned vert = s; // 이제 방문할 정점 : 아직 시작하지 않았으므로 시작점으로 초기화
    visited[0] = true; // 안 쓰는 인덱스 방문할 일 없게 미리 표시
    d[s].first = 0; // 시작점은 거리 0
    next_visit.push(make_pair(s, d[s].first));

    while (!next_visit.empty()) { // 다음 방문 정점 큐가 비어있지 않을 동안
        if (!visited[vert]) {
            visited[vert] = true; // 정점 방문
            vector<Edge<T>> v_edge = edges_from(vert); // 정점에 연결된 간선 가져오기

            for (auto& e : v_edge) {
                if (d[vert].first + e.w < d[e.to].first) { // 거리를 업데이트할 필요가 있을 때에만
                    d[e.to].first = d[vert].first + e.w; // 거리 업데이트
                    d[e.to].second = vert; // 직전 방문 정점 업데이트
                    next_visit.push(make_pair(e.to, d[e.to].first));
                }
            }
        }

        if (!next_visit.empty()) {
            pair<unsigned, unsigned> next = next_visit.top(); // (정점, 거리)
            next_visit.pop();
            vert = next.first;
        }
    }

    // 위에서 알아낸 최소 비용 거리와 직전 방문 정점을 이용해 모든 경로 찾기
    // 도착점인 i로부터 시작점인 s까지 거슬러 올라가는 방식으로 탐색
    for (unsigned i = 1; i <= v; i++) {
        unsigned dest = d[i].second; // 시작점 s에서 정점 i를 찾아가는 경로상에서, i를 방문하기 직전의 정점
        full_path[i].first = d[i].first; // s에서 i로 가는 최소 비용
        full_path[i].second.push_front(i); // 도착점 i 먼저 리스트에 추가
        while (dest != s) { // 시작점 s에 도달하면 종료
            full_path[i].second.push_front(dest); // 지금 방문하는 점을 경로 맨 앞에 추가
            dest = d[dest].second; // 시작점에서 지금 방문한 점으로 오기까지, 직전 방문 정점을 다음 방문지로 지정
        }
        if (i != s) // 위의 반복문은 시작점 s를 다음 방문지로 지정하면 종료되기 때문에 경로에 추가되지 않으므로, 현재 도착점이 시작점과 다르다면 경로에 추가해야 함
            full_path[i].second.push_front(s);
    }

    return full_path;
}
IT, Algorithm
지식 IT 과제 자료구조 그래프 다익스트라 dijkstra 알고리즘
이 기사는 저작권자의 CC BY-NC-ND 4.0 라이센스를 따릅니다.
최근 업데이트
바로가기