우리는 이걸 데이터 전처리라고 부르기로 했어요.
이 글의 목적
캐글에서 유리 종류 구분하는 모델 만들면서 공부했던 것들을 여기에 정리해보겠다. 데이터를 어떻게든 다듬어서 정확도를 올려보겠다고 별 걸 다 공부했는데 그건 다 효과가 없었고 속성 몇 개 지웠더니 정확도가 20%p나 올라버려서 허무했지.
전체 코드 보기 : https://www.kaggle.com/dapin1490/glass/notebook
노션에도 정리해 두었으니 많이들 봐주시라구요
참고 : 내가 이해한 대로 설명하는 것이니 틀린 부분이 있을 수 있다. 지적 환영!
이번 글 목차
1. 첨도와 왜도, 상관 관계
2. K겹 교차검증은 원 핫 벡터를 인자로 전달할 수 없다
다음 글 보기
- 데이터의 상태가 이상하다!
- 랜덤 언더, 오버 샘플링
- SMOTE 오버 샘플링
- ADASYN 오버 샘플링
- 클래스 별 차등 가중치 부여하기
- 꼭 결측치가 있어야만 속성을 삭제할 수 있는 건 아니다
1. 첨도와 왜도, 상관 관계
- 필요 라이브러리
1
2
3
import numpy as np
import pandas as pd
import seaborn as sns
- 첨도 : 데이터가 얼마나 한 지점에 몰려 있나? 를 나타낸다. 이 값이 클수록 데이터가 많이 몰려있다는 의미이고, 값이 작으면 데이터가 많이 퍼져있다는 뜻이다.
1
2
3
4
5
6
7
8
9
10
# 데이터셋의 속성 별 첨도 확인하기
print(data.kurtosis())
# 속성 'K'의 히스토그램 보기
import matplotlib.pyplot as plt # 그래프 보기
import seaborn as sns # 그래프 보기
sns.histplot(data['K'])
plt.show()
첨도가 54.7쯤 되면 아래와 같은 히스토그램을 볼 수 있다. 세로축의 Count는 값의 개수, 가로축의 K는 이 속성의 이름이다. 딱 봐도 대략 0.1과 0.7쯤에 거의 모든 값이 몰려 있는 것을 확인할 수 있다.
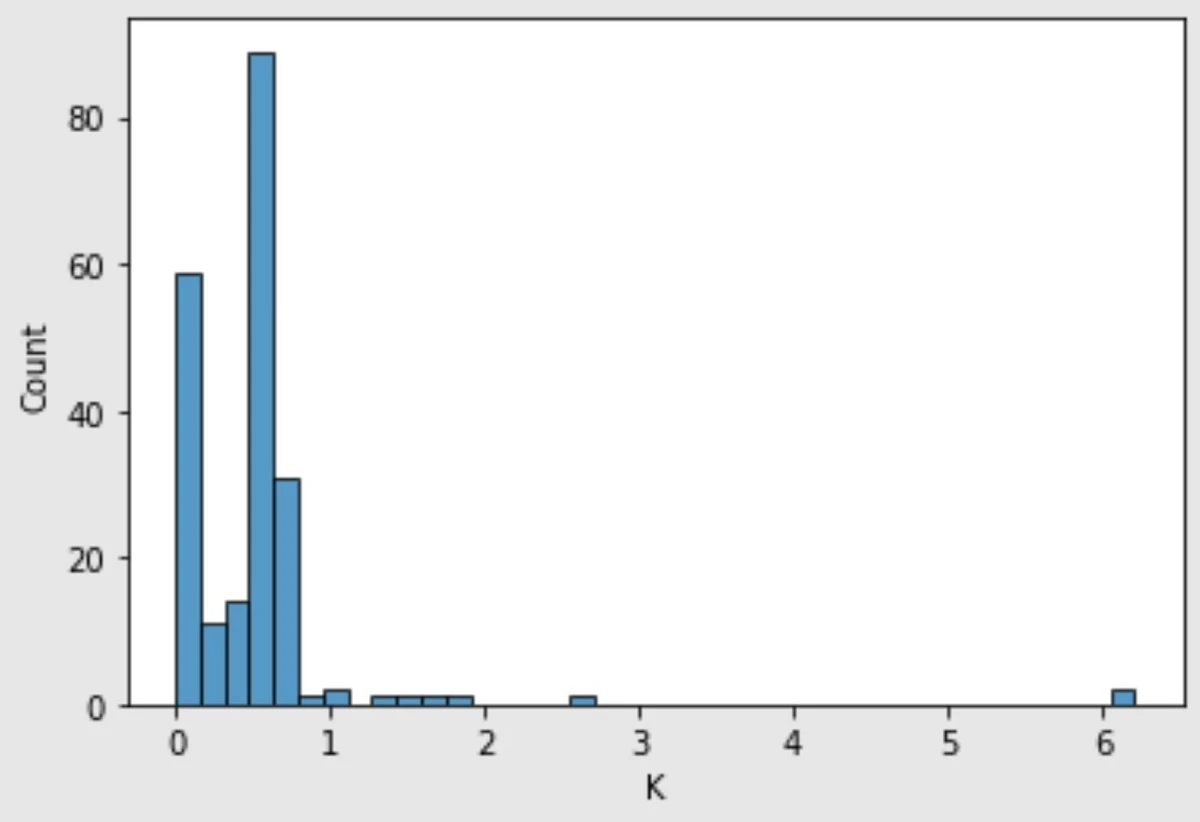
- 왜도 : 데이터가 얼마나 한 쪽에 치우쳐 있나? 를 나타낸다. 이 값이 양수이면 왼쪽에 치우쳐 있고(= 오른쪽 꼬리가 길고), 음수이면 오른쪽에 치우쳐 있다(= 왼쪽 꼬리가 길다). 요약하자면 절댓값이 클수록 꼬리가 길다.
1
2
# 속성 별 왜도 확인하기
print(data.skew())
위에서 확인했던 첨도가 약 54.7인 속성 ‘K’의 왜도는 약 6.6이다. 양수이고, 오른쪽에 자잘한 값이 길게 늘어지는 것을 [이미지 1]에서 확인할 수 있다.
- 첨도와 왜도는 뭐가 다르냐?
얼핏 보면 첨도나 왜도나 같은 말을 하는 것처럼 보일 수 있다. 하지만 잘 생각해 보면 분명한 차이가 있다. 정규분포를 가지고 이해해보자. 참고용으로 가져온 아래 그래프에서 빨간 그래프와 파란 그래프만을 본다. 빨간 그래프는 평균이 0, 분산이 1인 표준 정규 분포 그래프이다. 파란 그래프는 평균은 같지만 분산이 더 작다. 이 두 그래프의 첨도와 왜도는 어떻게 다를까?
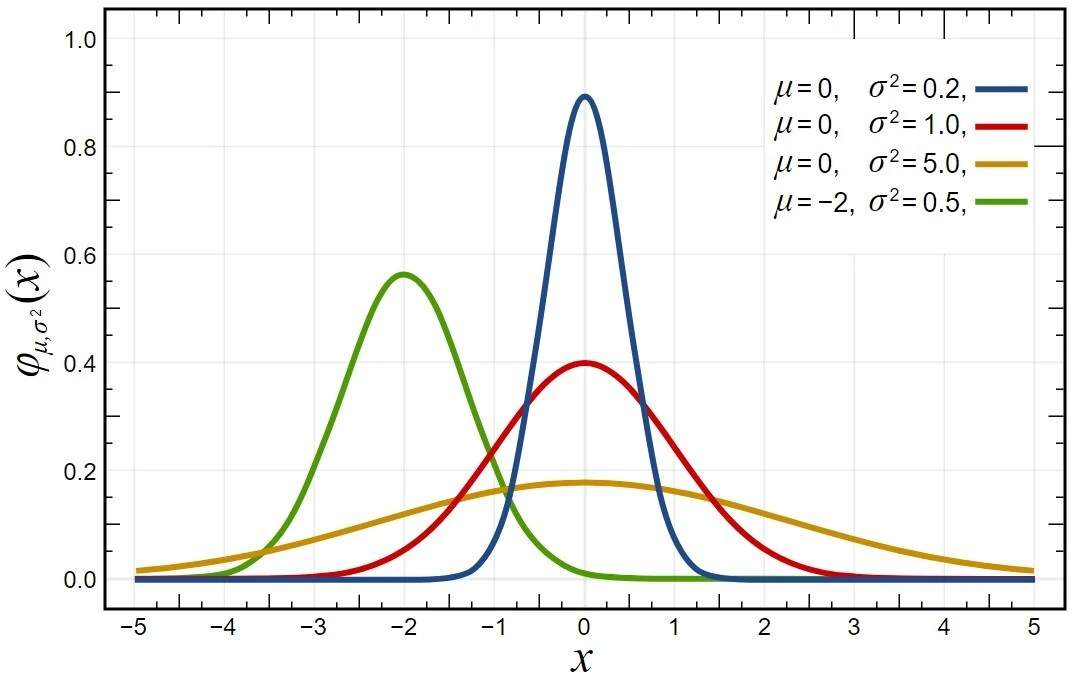
편의상 빨간 그래프를 A, 파란 그래프를 B라고 부르자. 첨도는 B가 더 크고, 왜도는 같다. 여기서 첨도와 왜도의 차이를 알 수 있다. 첨도는 값이 몰려 있는 지점이 어디든, 몰려 있기만 하면 무조건 커지는 값이다. 왜도는 값이 얼마나 몰려 있는지에 영향을 받을 수는 있지만 그게 가장 중요한 요인은 되지 못한다. 아무리 값이 한 지점에 몰린다 해도 좌우 대칭을 유지한다면 왜도는 영향을 받지 않는다. 왜도는 아까 괄호에 덧붙인 설명 그대로, 어느 쪽 꼬리가 더 긴지 나타내는 지표이다.
- 상관 관계 : 난 증가할 건데 넌 어느 쪽으로 가니? 라는 질문으로 이해할 수 있겠다. -1과 1 사이의 값을 가지며, -1에 가까울수록 반비례, 1에 가까울수록 정비례 관계이다. 첨도나 왜도와는 달리 무조건 값이 크다고 나쁜 것도 아니고 작다고 꼭 좋은 것도 아니다. 다만 알 수 있는 것은 절댓값이 작을 수록 상관 관계가 적다는 것이다.
1
2
3
4
5
6
7
8
9
10
11
# 클래스를 포함한 모든 속성 간의 상관 관계 수치로 확인하기
print(data.corr())
# 상관 관계 히트맵 보기
import matplotlib.pyplot as plt # 그래프 보기
import seaborn as sns # 그래프 보기
plt.figure(figsize=(10, 8))
sns.heatmap(data.corr(), annot=True, cmap="YlGnBu", vmax=1)
plt.show()
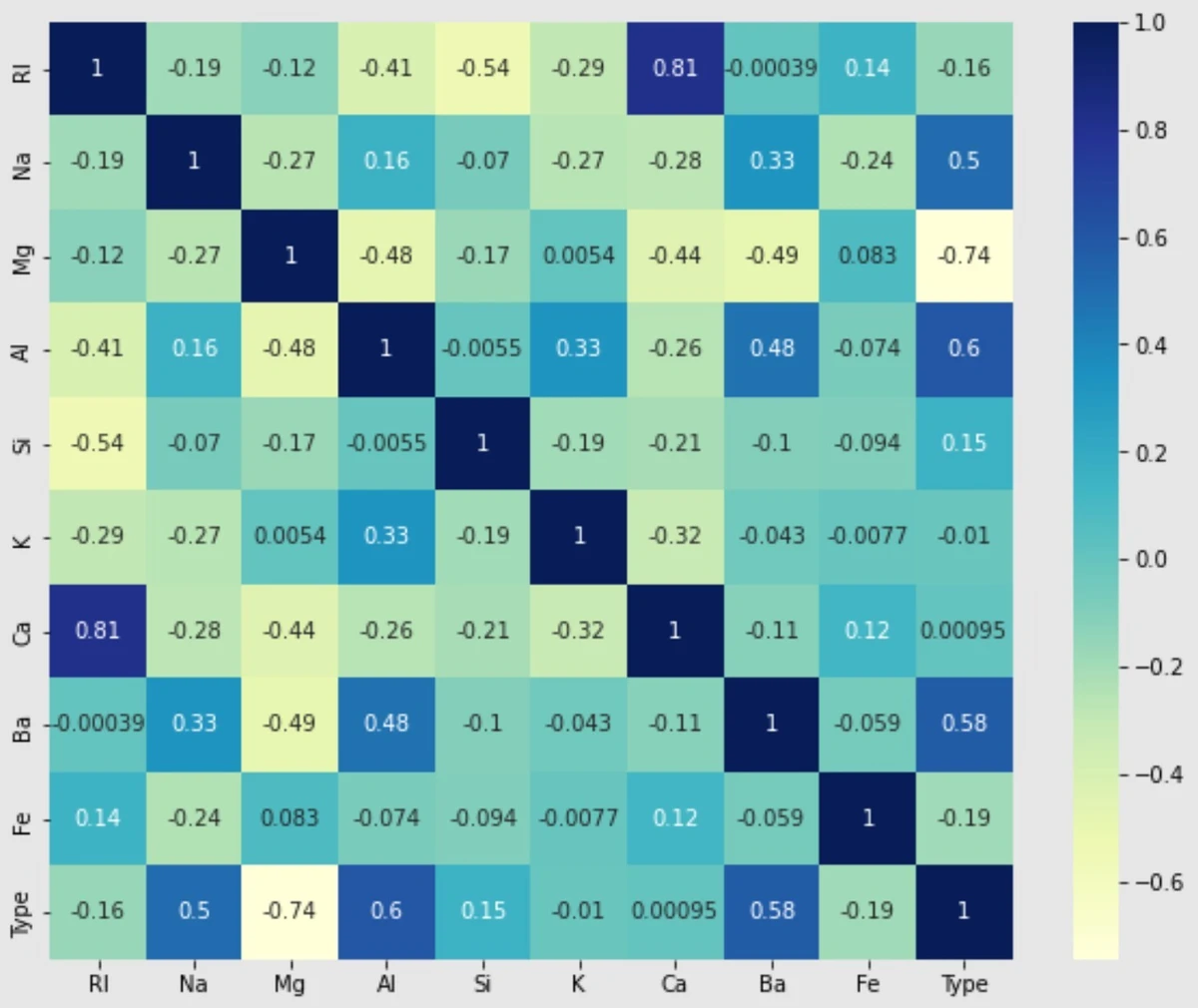
상관 관계는 숫자로 확인할 수도 있긴 하지만 히트맵으로 보면 훨씬 보기 좋다. 아래 히트맵은 상관 관계가 1에 가까울수록 진한 색을 띈다. Type가 클래스이니 맨아랫줄을 보거나 가장 오른쪽 줄을 보면 클래스와 다른 속성 간의 상관 관계를 알 수 있다. 클래스와 정비례 방향으로 상관 관계가 가장 높은 것은 속성 ‘Al’이고, 반비례 방향으로 상관 관계가 가장 높은 것은 속성 ‘Mg’이다. 어느 방향으로든 상관 관계가 가장 낮은 것은 속성 ‘Ca’이다.
2. K겹 교차검증은 원 핫 벡터를 인자로 전달할 수 없다
- K겹 교차검증 : 이번엔 내가 테스트 데이터 할게 다음엔 네가 테스트 데이터 해
딥러닝 모델을 훈련시키고 그 성과를 확인하려면 테스트를 시켜야 한다. 보통은 전체 데이터셋에서 테스트 데이터를 따로 분할해 놓고 쓰거나, 모델을 실행할 때 validation_split 인자를 주어 학습 과정에서 알아서 나누어 쓰도록 한다(두 가지 방법을 한 번에 사용하기도 한다). 그런데 세상이 아무리 정보가 넘쳐나는 세상이 되었다고 한들 학습에 필요한 데이터가 부족한 문제는 얼마든지 있을 수 있다. K겹 교차검증은 이럴 때 사용할 수 있다. 그림부터 보고 이해하자.
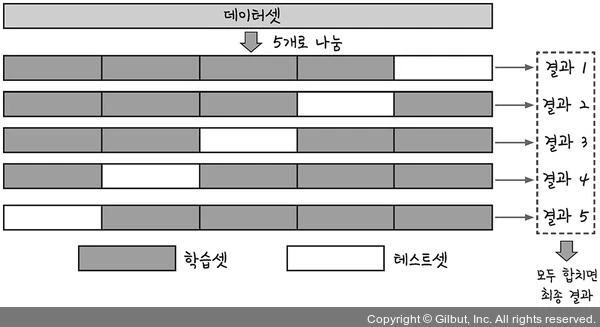
먼저 데이터셋을 프로그래머가 정한 개수(K개)로 나눈다. 그리고 그 중 하나씩을 테스트 데이터로 사용하며 총 K회 모델을 훈련시킨다. 각각의 테스트 결과로 나온 정확도를 평균내서 모델의 성능을 평가하는 방법이다. 모델을 아주 잘못 만든 게 아닌 이상 보통은 개별 결과가 서로 크게 차이나지 않는다.
- K겹 교차검증 코드 보기 : 코드 자체는 좀 간략하게 줄이려고 했는데 주석이 많아서 길어 보인다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# 라이브러리 불러오기
from keras.models import Sequential # 모델 선언, 구조 결정
from keras.layers import Dense # 모델에 층 추가
from sklearn.model_selection import StratifiedKFold # K겹 교차검증
# 교차검증 셋 분할
n_fold = 2 # 2개로 분할
# 분할 수는 최소 2개 이상 설정해야 한다.
# 1개로 설정할 거면 교차검증의 의미가 없으며, 오류가 난다.
# 난 그냥 모델 여러 번 실행해서 정확도 보기가 귀찮아서 이 방법을 쓴 거라 1로 해도 되는지 실행해봤다..
skf = StratifiedKFold(n_splits=n_fold, shuffle=True, random_state=seed)
# n_splits=n_fold : 데이터를 몇 개로 나눌 것인지 정함
# shuffle=True : 데이터를 섞어서 분할
# random_state=seed : 랜덤 시드 설정
# 빈 accuracy 배열 : K개의 테스트 정확도를 저장함
acc = []
# my model
for train, test in skf.split(X, Y):
model = Sequential()
model.add(Dense(15, input_dim=5, activation="relu"))
model.add(Dense(13, activation="relu"))
model.add(Dense(8, activation="softmax"))
# model compile
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=['accuracy'])
model.fit(X[train], Y[train], validation_split=0.3, epochs=1000, batch_size=60, verbose=1)
# validation_split=0.3 : 안 써도 된다. 학습 데이터 중 30%를 학습 중 모델의 테스트용으로 쓴다는 뜻이다.
k_acc = "%.4f" % (model.evaluate(X[test], Y[test])[1])
acc.append(k_acc)
# 결과 출력
# 주의 사항 : 일반적인 리스트가 아니기 때문에 mean()은 사용 불가하다.
print("\n %.f fold accuracy:" % n_fold, acc)
- 원 핫 인코딩, 원 핫 벡터 : 다른 건 보지 마 이게 정답이야 이것만 봐 좀
원 핫 인코딩은 예측해야 할 클래스가 선형 회귀가 아니고, 여러 개일 때 사용할 수 있는 방법이다. 예를 들어 0번부터 3번까지 클래스가 3개 있다고 하자. 프로그래머는 딥러닝 모델에게 이 클래스를 그대로 [0, 1, 2, 3]라고 전달할 수 있다. 그러나 보통은 원 핫 인코딩을 거쳐 [ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1] ] 이런 형태로 전달한다. 이렇게 정답 클래스의 인덱스만 1로 표시하고 나머지는 0으로 표시하는 것이 원 핫 인코딩이다. 그리고 원 핫 인코딩을 한 클래스 각각을 원 핫 벡터라고 한다.
- 원 핫 벡터의 길이 : 누가 여기서 가장 크냐?
방금 예시에서는 클래스가 0부터 3까지 있었다. 그럼 만약 클래스가 1과 3만 있는 데이터를 원 핫 인코딩 한다면 어떻게 될까? 사람 기준에서는 어차피 둘 중 하나이니 [ [1, 0], [0, 1] ] 이렇게만 만들면 될 것 같지만 실제로 원 핫 인코딩을 해보면 위의 예시와 똑같은 결과가 나온다. 이유는 원 핫 인코딩이 표시하는 것이 클래스의 상대적 순서가 아니라, 인덱스 자체이기 때문이다. 파이썬의 인덱스는 0부터 시작하니, 정수로 표시된 클래스들 중 가장 큰 수를 받은 클래스의 숫자 + 1이 원 핫 벡터의 길이가 되고, 동시에 그것이 출력층의 노드 개수가 된다(클래스의 인덱스를 음수로 주는 경우는 본 적이 없다). 이는 자연어 처리에서도 똑같이 적용된다만, 지금 정리할 개념은 아니니 언급만 해둔다.
- 원 핫 인코딩 왜 함?
원 핫 벡터에 사용되는 숫자와 클래스에 매겨지는 인덱스에 사용되는 숫자를 생각해 보자. 클래스 인덱스는 10진수로 매겨진다. 원 핫 벡터는 0과 1만 사용하니 2진수라고 할 수 있겠다. 10진수와 2진수의 차이가 뭘까? 10진수는 산수가 되고 2진수는 안 된다는 점이다. 10진수인 1과 2를 더하면 3이 되지만 원 핫 벡터는 모든 값을 0과 1로만 표시하면서 그런 계산을 불가능하게 만들었다. 이 부분이 원 핫 인코딩의 장점이자 단점이다.
사람은 데이터의 의미를 이해할 수 있으니 1번 클래스와 2번 클래스를 더하는 것과 3번 클래스는 무관하다는 사실을 인지할 수 있다. 하지만 모델은 그런 생각을 할 수 없다. 그렇기 때문에 클래스의 인덱스를 10진수로 주면 1 + 2 = 3이니까 1번 클래스와 2번 클래스를 더하면 3번 클래스와 같을 거라는 잘못된 학습을 할 수도 있다. 원 핫 인코딩은 이 문제를 방지한다. 이것이 장점이다.
반면 실제로 1번 클래스와 2번 클래스의 합이 3번 클래스와 관계가 있는 데이터도 있을 수 있다. 예를 들면 자연어 처리가 그러하다. 하나의 문장 내에서 각각의 단어는 무관하지 않다. “오늘 날씨”와 “내일 날씨”는 같은 “날씨”를 요구한다고 해도 다르게 해석되어야 한다. 원 핫 인코딩은 이런 관계성을 차단하여 클래스 사이의 유사성도 나타내지 못하게 된다는 것이 단점이다.
- K겹 교차검증에 원 핫 인코딩을 못쓴다고?
K겹 교차검증은 데이터 전체를 우선 K개의 세트로 분할한 후 모델에 주어 학습시킨다. 이때 클래스는 원 핫 벡터 형태로 넘겨줄 수 없다. 이유까지 아는 것은 아니고, 오류가 떠서 알게 된 사실이다.
그렇다면 K겹 교차검증을 하려거든 원 핫 인코딩을 포기해야 할까? 다행히도 그렇지는 않다. 데이터셋을 먼저 분할하여 반복문 내에 진입한 후, 그 안에서 원 핫 인코딩을 실행하면 된다. 그게 다다!
- K겹 교차검증과 원 핫 인코딩 : 이제와서 밝히지만 위의 K겹 교차검증 코드는 이 코드에서 원 핫 인코딩 부분만 지운 것이라 그대로 실행하면 오류가 발생할 수 있다. 그건 참고로만 보자. 이 코드는 실행 가능하다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# make model
from keras.models import Sequential # 모델 선언, 구조 결정
from keras.layers import Dense # 모델에 층 추가
from sklearn.model_selection import StratifiedKFold # K겹 교차검증
# 교차검증 셋 분할
n_fold = 2
skf = StratifiedKFold(n_splits=n_fold, shuffle=True, random_state=seed)
# 빈 accuracy 배열
acc = []
from keras.utils import np_utils # 원 핫 인코딩
# my model
for train, test in skf.split(X, Y):
# 분할되어 들어온 클래스 데이터를 원 핫 인코딩 한다.
Y_one_tr = np_utils.to_categorical(Y[train])
Y_one_te = np_utils.to_categorical(Y[test])
# 이후는 전과 같다.
model = Sequential()
model.add(Dense(15, input_dim=5, activation="relu"))
model.add(Dense(13, activation="relu"))
model.add(Dense(8, activation="softmax"))
# model compile
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=['accuracy'])
model.fit(X[train], Y_one_tr, validation_split=0.3, epochs=1000, batch_size=60, verbose=1)
k_acc = "%.4f" % (model.evaluate(X[test], Y_one_te)[1])
acc.append(k_acc)
# 결과 출력
print("\n %.f fold accuracy:" % n_fold, acc)
