홈 [자료구조] BFS와 DFS
포스트
취소

[자료구조] BFS와 DFS

게시 2022-11-07
By dapin1490
23 분읽는 시간

할 일

이번 숙제는 다음 내용을 포함합니다.
1. 그래프 예시를 직접 만듭니다. (O)
2. BFS와 DFS 알고리즘을 바탕으로 그래프 탐색 과정을 그립니다. (O)
3. 본인이 편하게 사용할 수 있는 BFS와 DFS 코드를 작성합니다. (O)
4. (옵션) BFS 관련 문제를 풀어 봅니다. (X)

DFS 관련 문제는 금일 시간 관계 상 다루지 못하였기 때문에 다음 주에 다룹니다. 

평가(총 6점)
3점: 독자 입장에서 평가 대상 수강생의 포트폴리오를 읽고, BFS 과정을 쉽게 이해할 수 있는지
3점: 독자 입장에서 평가 대상 수강생의 포트폴리오를 읽고, DFS 과정을 쉽게 이해할 수 있는지
보너스 점수 항목:
첫째. BFS와 DFS의 차이점을 알 수 있는지
둘째. BFS 관련 문제 풀이를 통해 알고리즘을 적용해 보았는지

목차

  1. 그래프
  2. BFS 알고리즘과 코드
  3. DFS 알고리즘과 코드 - 미완성
  4. BFS와 DFS의 시각적 비교

그래프

그래프(graph) G=(V, E)는 유한한 개수의 정점(vertex) 또는 노드(node)들의 집합인 V와 연결선(edge) 또는 에지라고 불리는 정점들의 쌍들의 집합인 E로 이루어진다.[1]

쾨니히스베르크 다리 문제(위키백과)를 들어본 적이 있다면 금방 이해할 수 있을 것이다. 프로그래밍에서 말하는 그래프는 엑셀에 그리는 것과 같은 그래프가 아니고, 선으로 연결된 점들의 집합이다.

그래프는 크게 방향이 있는 것과 방향이 없는 것으로 나눌 수 있다. 보통 그래프라고 하면 방향이 없는 그래프를 의미하며 방향이 있는 그래프는 방향 그래프(directed graph) 또는 다이그래프(digraph)라고 따로 지칭한다. 이때 간선은 아크(arc)라고 말한다.[1] 이 글에서도 그래프라고 하면 기본적으로 방향이 없는 그래프를 지칭한다. 덧붙여, 트리도 그래프의 일종이다. 자세한 것은 참고 자료 1번의 책을 공부하자.

그래프의 예시는 아래와 같다. 이후에 BFS와 DFS를 설명할 때에도 사용할 그래프이니 잘 봐두자.

[이미지 1] 그래프 예시

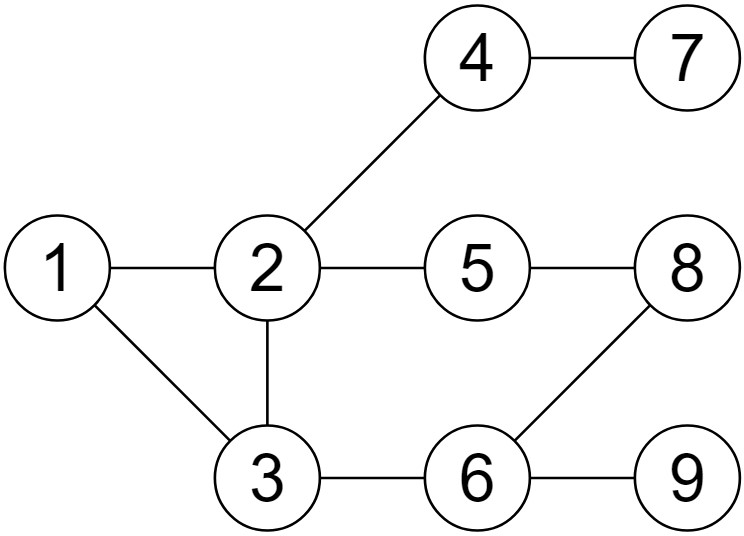
BFS 알고리즘과 코드

BFS는 Breadth First Search의 약자로 너비 우선 탐색이라고 한다. 특정한 시작점에서 출발하여, 그 점에서 가장 가까운 점부터 차례대로 방문한다. 시작점을 중심으로 동심원을 그려나간다고 생각하면 이해하기 좋다. 매번 정점을 방문할 때마다 다음에 방문할 정점을 저장해두고 저장한 순서대로 방문하기 때문에, 이 알고리즘을 수행할 때는 큐를 사용하는 것이 적절하다. 그리고 비선형 구조를 탐색하는 것이기 때문에 한 번 탐색한 곳을 다시 탐색하지 않는 것이 중요하다. 이를 위해 방문한 정점의 배열을 따로 만들어 사용한다.

이 알고리즘을 정리하면 다음과 같다.

시작점을 큐에 넣고, 방문했음을 표시한다.
이후의 과정을 큐가 비어있을 때까지 반복한다:
    큐에서 요소를 하나 pop하고 방문했음을 표시한다.
    방금 pop한 것에 대하여 방문하지 않은 정점만 큐에 push한다.

[이미지 1]을 예시로 BFS 탐색을 수행해보자. 시작점은 1이고 거리가 같은 정점이 여러 개 있을 때는 숫자가 작은 것부터 방문한다고 가정한다.

  1. 탐색을 시작하기 전, 방문해야 할 정점을 저장할 빈 큐와 모든 정점의 방문 여부가 false로 표기된 방문 정점 리스트를 준비한다. 이 리스트는 배열을 써도 좋고, 벡터를 써도 좋다.
    • 큐의 내용 : (비어있음)
    • 방문 정점 리스트 : { 0, 0, 0, 0, 0, 0, 0, 0, 0 } // 편의상 true/false 대신 1/0으로 표기하며, 인덱스는 1부터 시작한다.
  2. 탐색을 시작한다. 가장 먼저 시작점인 1을 큐에 넣고 방문했음을 표시한다.
    • 큐의 내용 : { 1 }
    • 방문 정점 리스트 : { 0, 0, 0, 0, 0, 0, 0, 0, 0 }
  3. 큐에 저장된 것을 하나 꺼낸다. 2번에서 1을 큐에 넣었으므로 1이 나온다. 1과 인접한 정점들을 큐에 차례대로 넣는다. 여기서는 2와 3을 넣으면 된다.
    • 큐의 내용 : { 2, 3 }
    • 방문 정점 리스트 : { 1, 0, 0, 0, 0, 0, 0, 0, 0 }
  4. 큐에 저장된 것을 하나 꺼내고(2가 나온다), 아직 방문하지 않은 정점이므로 해당 정점을 방문한 것으로 표시한다.
    • 큐의 내용 : { 3 }
    • 방문 정점 리스트 : { 1, 1, 0, 0, 0, 0, 0, 0, 0 }
  5. 2와 인접한 정점들 중 방문하지 않은 것들을 큐에 차례대로 넣는다. 4, 5가 큐에 들어간다.
    • 큐의 내용 : { 4, 5 }
    • 방문 정점 리스트 : { 1, 1, 0, 0, 0, 0, 0, 0, 0 }
  6. 위의 과정을 더이상 방문할 정점이 없을 때까지 수행한다.

[이미지 1]의 그래프를 위와 같은 과정으로 탐색하면 방문하는 노드의 순서는 { 1, 2, 3, 4, 5, 6, 7, 8, 9 }이다. 그림으로 그리면 아래와 같다. 노란색, 초록색, 파란색, 보라색 영역 내에 있는 정점을 순서대로 방문한다.

[이미지 2] BFS 예시

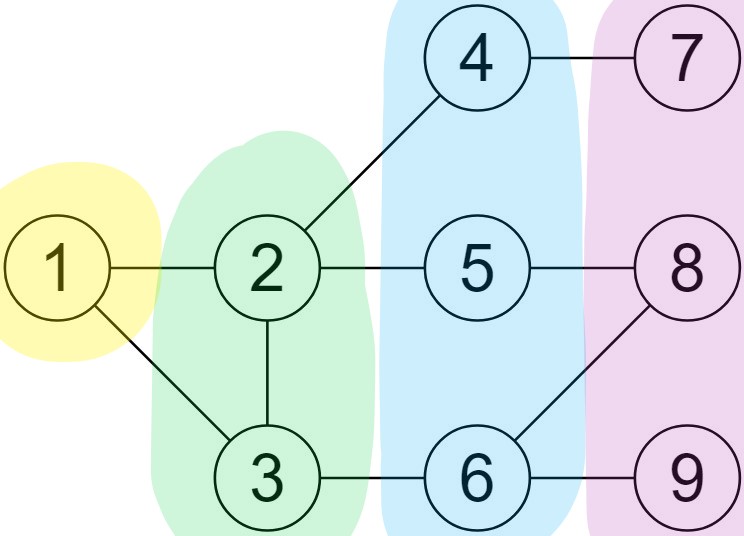
코드로 구현해보자. 위에 서술된 알고리즘과는 약간 다른 부분이 보일 수 있는데, BFS 알고리즘을 이용해 시작점(station)을 기준으로 시작점과 각 정점 간의 거리를 구하는 코드이다. 인접한 정점 간의 거리는 모두 1로 전제한다. 또한 cout을 이용한 출력 대신 별도의 텍스트파일에 결과를 쓰도록 했다. cout으로 실행하고 싶다면 output_file을 모두 cout으로 바꿔쓰면 된다. 전체 코드는 깃허브에서 볼 수 있으며, 교수님의 코드를 참고하여 내 방식대로 작성한 것이다. 전체 코드의 길이가 길어 아래 코드는 일부 생략하고 작성했다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

struct Node {
    int to_station = INFINITY; // 가장 가까운 station까지의 거리
    vector<int> adj; // 인접 노드
    vector<int> d; // 각 인접 노드까지의 거리
};

class Graph {
private:
    int vertices; // 점 수
    vector<Node> graph; // 각 노드의 키값은 벡터의 인덱스로 대체
    vector<bool> visited; // 방문 여부

    void print_route(); // BFS로 탐색 후 탐색 결과를 출력함

public:
    Graph(int vts); // 생성자

    void BFS(int start_key);
    void BFS(vector<int> starts); // station이 여러 개일 경우 사용, 코드는 생략
};

void Graph::BFS(int start_key) { // 루트(시작점)에서 시작
    queue<int> que;
    graph[start_key].to_station = 0; // 시작점은 station이므로 station까지의 거리가 0
    visited[start_key] = true; // 방문 표시 후
    que.push(start_key); // 큐에 push

    output_file << "----------\nStation : " << start_key << "\nSearch by BFS\n\n";

    while (!que.empty()) { // 큐가 비어있을 때까지
        start_key = que.front(); // 큐에서 하나 pop
        que.pop();

        int len = graph[start_key].adj.size();
        for (int i = 0; i < len; i++) { // 방금 pop한 노드의 인접한 노드에 대해 방문하지 않은 것에 한해 큐에 push
            int current = graph[start_key].adj[i];
            if (!visited[current]) {
                visited[current] = true;
                que.push(current);
                graph[current].to_station = graph[start_key].to_station + 1; // 지금 방문한 곳은 station으로부터 현재의 기준점보다 1만큼 더 떨어져 있음
            }
        }
    }

    // 탐색을 끝낸 후 방문 여부 표시를 모두 지움
    visited.assign(vertices, false);

    // 탐색 결과 출력
    this->print_route();
    output_file << "----------\n";
}

DFS 알고리즘과 코드

DFS는 Depth First Search의 약자로 깊이 우선 탐색이라고 한다. 특정한 시작점에서 출발하여, 그 점에서 갈 수 있는 가장 깊은 점부터 차례대로 방문한다. 미로에서 출구를 찾을 때의 풀이 과정을 생각하면 된다. 보통 사람은 동시에 여러 통로를 볼 수 없기 때문에, 하나의 통로를 쭉 따라가 그것의 끝이 막혔는지 확인하고, 막혔다면 되돌아와 다른 갈림길로 들어가 같은 과정을 반복하는 방식으로 미로를 탐색한다. 이것이 DFS의 방식이다. 더이상 갈 곳이 없을 때까지 나아간 후, 되돌아 나오면서 등장하는 갈림길에서 다시 가장 깊은 곳으로 들어가는 것을 반복하여 탐색한다. DFS는 나아간 길을 되돌아올 수 있어야 하기 때문에 재귀나 스택을 사용하는 게 적절하다. BFS와 마찬가지로 한 번 방문한 곳을 다시 방문하지 않는 것이 중요하다.

이 알고리즘을 정리하면 다음과 같다. 재귀로 구현하는 방법도 있으나, 이 글에서는 스택을 사용하는 방식으로 구현하였다.

시작점을 스택에 넣는다.
이후의 과정을 스택이 비어있을 때까지 반복한다:
    스택에서 요소를 하나 pop한다.
    방금 pop한 정점이 아직 방문하지 않은 정점일 경우에만 아래 과정을 수행한다:
        현재 정점을 방문한 것으로 표시한다.
        현재 정점의 인접한 정점을 모두 스택에 push한다.

[이미지 1]을 예시로 DFS 탐색을 수행해보자. 시작점은 1이고 거리가 같은 정점이 여러 개 있을 때는 숫자가 작은 것부터 스택에 넣는다. 그러므로 실제 방문 순서는 숫자가 큰 것부터 방문하게 된다. 스택 push 순서를 바꾸면 작은 것부터 방문하도록 할 수 있다.

  1. 탐색을 시작하기 전, 방문해야 할 정점을 저장할 빈 스택과 모든 정점의 방문 여부가 false로 표기된 방문 정점 리스트를 준비한다. 이 리스트는 배열을 써도 좋고, 벡터를 써도 좋다.
    • 스택의 내용 : (비어있음)
    • 방문 정점 리스트 : { 0, 0, 0, 0, 0, 0, 0, 0, 0 } // 편의상 true/false 대신 1/0으로 표기하며, 인덱스는 1부터 시작한다.
  2. 탐색을 시작한다. 가장 먼저 시작점인 1을 스택에 넣는다.
    • 스택의 내용 : { 1 }
    • 방문 정점 리스트 : { 0, 0, 0, 0, 0, 0, 0, 0, 0 }
  3. 스택에 저장된 것을 하나 꺼낸다. 2번에서 1을 넣었으므로 1이 나온다. 1은 아직 방문하지 않은 정점이므로 방문한 것으로 표시하고, 1과 인접한 정점들을 스택에 차례대로 넣는다. 여기서는 2와 3을 넣으면 된다.
    • 스택의 내용 : { 3, 2 }
    • 방문 정점 리스트 : { 1, 0, 0, 0, 0, 0, 0, 0, 0 }
  4. 스택에 저장된 것을 하나 꺼내고(3이 나온다), 아직 방문하지 않은 정점이므로 해당 정점을 방문한 것으로 표시한다. 이후 3과 인접한 정점들을 스택에 넣는다. 1, 2, 6이 스택에 들어간다. 만약 이미 방문한 정점이 스택에서 나왔다면 아무것도 하지 않고 넘어간다.
    • 스택의 내용 : { 6, 2, 1, 2 }
    • 방문 정점 리스트 : { 1, 0, 1, 0, 0, 0, 0, 0, 0 }
  5. 위의 과정을 더이상 방문할 정점이 없을 때까지 수행한다.

[이미지 1]의 그래프를 위와 같은 과정으로 탐색하면 방문하는 노드의 순서는 { 1, 3, 6, 9, 8, 5, 2, 4, 7 }이다. 그림으로 그리면 아래와 같다. 노란색, 초록색, 파란색, 보라색 영역 내에 있는 정점을 순서대로 방문한다.

[이미지 3] DFS 예시

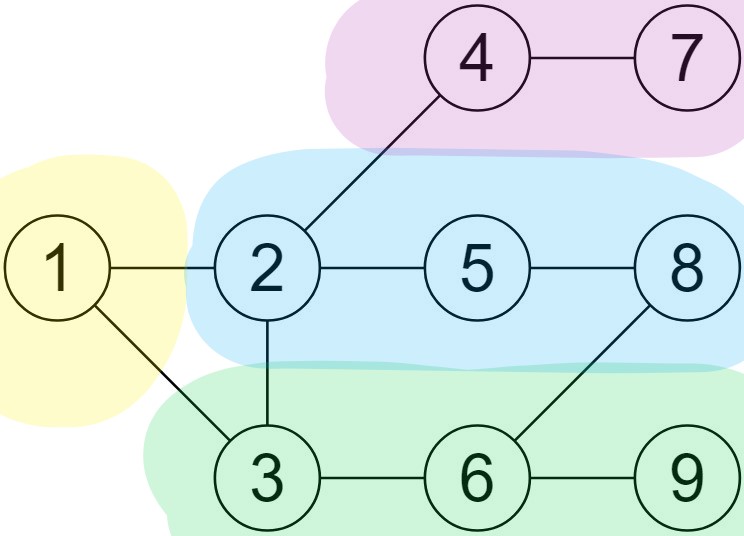
코드로 구현해보자. BFS와 마찬가지로 시작점을 기준으로 각 정점까지의 거리를 구하는 코드를 작성하려고 했으나, DFS 탐색은 할 수 있지만 거리는 적절하게 구하지 못하는 결과가 나왔다. DFS 코드는 참고 자료 [2]를 참고하여 작성했다. 출력 방식과 전체 코드 링크는 BFS와 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

struct Node {
    int to_station = INFINITY; // 가장 가까운 station까지의 거리
    vector<int> adj; // 인접 노드
    vector<int> d; // 각 인접 노드까지의 거리
};

class Graph {
private:
    int vertices; // 정점 수
    vector<Node> graph; // 각 노드의 키값은 벡터의 인덱스로 대체
    vector<bool> visited; // 방문 여부

    void print_route();

public:
    Graph(int vts); // 생성자

    // 반복으로 구현한 DFS
    void DFS_by_iteration(int start_key);
    void DFS_by_iteration(vector<int> starts); // 시작점이 여러 개일 경우, 코드는 생략

    // 재귀로 구현한 DFS, 코드는 생략
    void DFS_by_recursion(int start_key, bool is_start = true);
    void DFS_by_recursion(vector<int> starts, bool is_start = true); // 시작점이 여러 개일 경우
};

void Graph::DFS_by_iteration(int start_key) { // 루트(시작점)에서 시작
    stack<pair<int, int>> s; // first는 방문해야 할 노드, second는 직전에 방문한 노드

    s.emplace(start_key, start_key);
    graph[start_key].to_station = -1; // 시작점은 station이므로 station까지의 거리가 0인데, 절차상 while 안에서 한번 방문하고 +1을 해야 하기 때문에 -1로 초기화

    output_file << "----------\nStation : " << start_key << "\nSearch by DFS(iteration)\n\n";

    while (!s.empty()) {
        pair<int, int> curr = s.top(); // 스택에서 pop
        s.pop();

        if (!visited[curr.first]) { // pop한 정점이 아직 방문하지 않은 것일 때
            visited[curr.first] = true; // 방문 표시
            graph[curr.first].to_station = graph[curr.second].to_station + 1; // 거리 합산
            output_file << "visit : " << curr.first << "\n"; // 방문한 노드를 출력

            for (vector<int>::iterator i = graph[curr.first].adj.begin(); i != graph[curr.first].adj.end(); i++) {
                s.emplace(*i, curr.first); // 인접 노드를 전부 스택에 추가
            }
        }
    }

    // 탐색을 끝낸 후 방문 여부 표시를 모두 지움
    visited.assign(vertices, false);

    // 탐색 결과 출력
    this->print_route();
    output_file << "----------\n";
}

BFS와 DFS의 시각적 비교

지금까지 하나의 그래프를 BFS와 DFS로 탐색하며 두 알고리즘의 개념을 익혔다. 그렇지만 아무래도 두 개념은 헷갈리기가 쉽다. 그래서 위에서 사용한 두 알고리즘의 탐색 순서를 색깔로 표현한 이미지를 같이 붙여보았다. 왼쪽이 BFS, 오른쪽이 DFS이다. 그림의 가로 세로 방향보다는, 노란색으로 칠해진 시작점을 기준으로 어떻게 나아가는지를 보면 좋다. 시작점으로부터 짧게 겹겹이 나아가는 것이 BFS, 길고 깊게 나아가는 것이 DFS이다. 두 이미지 모두 탐색은 노란색 → 초록색 → 파란색 → 보라색 순서로 진행한다.

[이미지 2] BFS 예시
[이미지 3] DFS 예시

참고 자료

[1] 『4차 산업혁명 시대의 이산수학』, 김대수 지음, 생능출판
[2] DFS / BFS 예제 구현해보기 - python, https://nareunhagae.tistory.com/17
[3] C++ 파일 읽기/쓰기(C++ File Read/Write Example), https://jdm.kr/blog/170
[4] C++에서 현재 시간 및 날짜 가져오기, https://www.techiedelight.com/ko/get-current-time-and-date-in-cpp/
[5] C++ - localtime_s 사용 예, https://jacking75.github.io/C++_localtime_s/
[6] #pragma once 가 모든 문제를 해결해주진 않는다, https://teus.me/819
[7] [C언어][헤더 파일 중복 방지] #pragma once, #ifndef, https://blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=white_cap&logNo=221002699804
[8] [C, C++] #include <헤더파일>과 #include “헤더파일”의 차이, https://shjz.tistory.com/97

IT, Algorithm
지식 IT 과제 BFS DFS 탐색 그래프 자료구조 알고리즘
이 기사는 저작권자의 CC BY-NC-ND 4.0 라이센스를 따릅니다.
최근 업데이트
바로가기