할 일
아래 내용을 포함하는 포트폴리오를 작성하고, 웹페이지 주소를 제출합니다.
1. 벨만포드 알고리즘 정리 (O)
2. Leet code 문제 풀이 : 743번 네트워크 딜레이 시간 (O)
https://leetcode.com/problems/network-delay-time/
2.1. 다익스트라를 이용한 풀이 (O)
2.2. 벨만포드를 이용한 풀이 (O)
3. 백준 문제 풀이: 1916번(옵션) (X)
https://www.acmicpc.net/problem/1916
3.1. 다익스트라를 이용한 풀이 (X)
3.2. 벨만포드를 이용한 풀이 (X)
목차
- 벨만-포드 알고리즘
- 문제 풀이 - Leet code 743 네트워크 딜레이 시간
벨만-포드 알고리즘
음수 가중치를 사용할 수 없는 다익스트라와 달리 음수 가중치에도 대응할 수 있는 최단 경로 탐색 알고리즘이다. 전체 정점 수보다 1 적은 수만큼, 매 번의 반복마다 모든 간선을 확인해 최단거리를 구한다. 음수 사이클이 존재할 경우 해를 구할 수 없다.
알고리즘 수행 과정은 다음과 같다.
1
2
3
4
5
1. 출발점을 정하고 최단거리 배열을 초기화한다.
2. 아래 과정을 (정점 수 - 1)만큼 반복한다.
- 모든 간선을 하나씩 확인하며
- 각 간선을 거쳐 다른 노드로 가능 비용을 계산해 최단거리 배열을 업데이트한다.
3. 반복을 끝낸 후 위의 과정을 다시 한 번 수행하고, 만약 최단거리 배열이 새로 업데이트된다면 경로를 찾을 수 없는 것이다.
음수 사이클에 대해 좀 더 생각해 보자. 벨만-포드 알고리즘은 음수도 다룰 수 있다는 것이 장점이지만 사이클을 검사하지 않고, 해를 찾는 과정에서 사이클이 생길 수 있다는 문제가 있다. 모든 가중치가 양수였다면 사이클은 당연히 손해로 판단되어 경로에 포함되지 않겠지만 사이클에 음수가 있다면 사이클을 돌 때마다 비용이 줄어드는 경로가 발견될 수 있다.
벨만-포드 알고리즘에서 경로 탐색을 끝낸 후 같은 과정을 다시 한번 수행하는 것은 돌 때마다 비용이 감소하는 음수 사이클의 특징을 이용해 사이클을 찾아내는 것이다. 음수 사이클이 존재한다면 벨만-포드 알고리즘으로는 최단경로를 구할 수 없다. 꼭 구해야 한다면, 모든 가중치에 같은 값을 더해 전부 양수로 만들고 다익스트라를 수행하면 된다.
23.04.19 수정
가중치에 충분히 큰 양수를 더해 그대로 다익스트라를 수행해도 최단경로는 찾을 수 없다. 간단한 반례를 보자. 출발점은 A이고 도착점은 C이다.
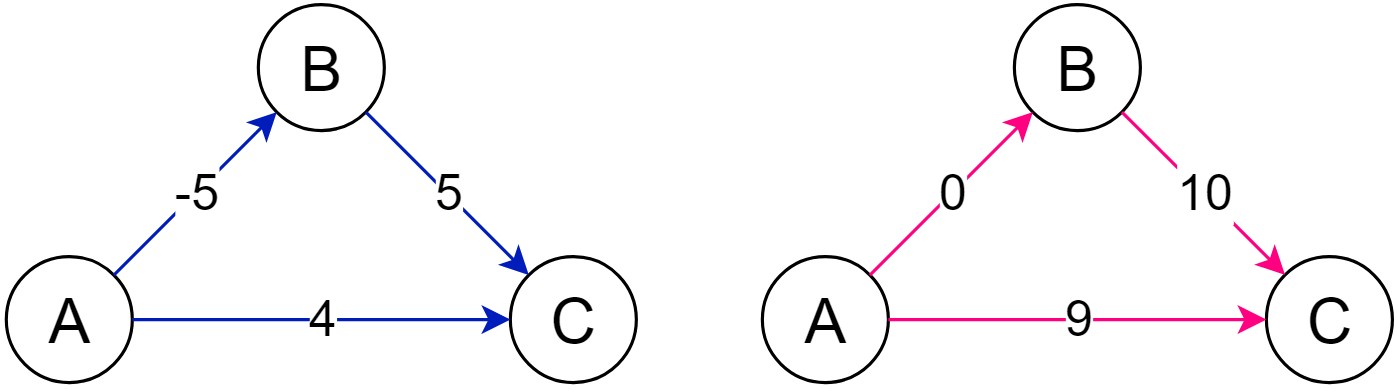
왼쪽 그래프의 최단경로는 A → B → C이고 오른쪽의 최단경로는 A → C이다. 모든 간선에 똑같이 5를 더해 전부 양수로 만들었을 뿐인데 최단경로가 달라졌다. 왜 달라졌을까?
이유는 최단경로를 이루는 간선의 개수에 있다. 왼쪽 그래프의 최단 경로는 2개의 간선으로 이루어졌고, 오른쪽 그래프의 최단 경로는 1개의 간선으로 이루어졌다. 각 간선마다 5의 가중치를 더했기 때문에 왼쪽 그래프의 최단경로에는 총 10의 가중치가 더해졌고, 오른쪽 그래프의 최단경로에는 총 5의 가중치가 더해진 셈이다. 모든 간선에 “똑같이” 더한다고 했지만 결과적으로는 똑같지 않았다는 말이다. 다시 말해 왼쪽 그래프와 오른쪽 그래프는 의미상으로 전혀 다른 그래프가 되었기 때문에 최단경로도 달라질 수밖에 없다는 것이다.
그렇다면 음수 가중치를 잘 없앨 수 있는 방법은 없을까? 있긴 하다. 존슨 알고리즘이라고 한다. 그래프에 없던 정점을 하나 추가하고 벨만포드와 다익스트라를 결합하여, 음수 가중치를 다루지 못하는 다익스트라의 문제를 해결했다. 자세한 설명은 이 글에서는 하지 않는다.
벨만-포드 알고리즘을 코드로 구현하면 아래와 같이 쓸 수 있다. 체감상 다익스트라보다 짧고 이해하기 쉽다. 전체 코드는 깃허브에서 확인할 수 있다. 쓰는 김에 다익스트라도 같이 썼는데, 그건 덤이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 벨만-포드
vector<int> route_search::bellman(int s) { // s는 시작점
dist.assign(vnum + 1, INT_MAX); // 클래스 멤버, 최단거리 벡터. 정점 번호가 1부터 시작함
dist[s] = 0; // 시작점은 거리 0
dist[0] = INT_MIN; // 안 쓰는 정점 표시
// 최단거리 구하기
for (int i = 1; i < vnum; i++) { // (정점 수 - 1)만큼 반복
for (auto& e : graph) { // 그래프에 존재하는 모든 간선에 대해
dist[e.to] = dist[e.to] > dist[e.from] + e.w ? dist[e.from] + e.w : dist[e.to]; // 짧으면 업데이트
}
}
// 음수 사이클 확인 : 위와 같은 과정이지만 업데이트 대신 return
for (int i = 1; i < vnum; i++) {
for (auto& e : graph) {
if (dist[e.to] > dist[e.from] + e.w) {
cout << "error_non-parametical: 경로상에 음수 사이클 존재\n";
dist.assign(vnum + 1, -1);
return dist;
}
}
}
return dist; // 음수 사이클을 통과했다면 정상적으로 최단거리를 구한 벡터 반환
}
문제 풀이 - Leet code 743 네트워크 딜레이 시간
문제 번역(파파고 번역 후 수정)
n개의 노드로 구성되고 1부터 n까지 레이블이 지정된 네트워크가 제공된다. 또한 times[i] = (u_i, v_i, w_i)와 같은 이동 시간이 지정된 방향 간선 목록이 제공된다. 여기서 u_i는 소스 노드, v_i는 대상 노드, w_i는 신호가 소스에서 대상으로 이동하는 데 걸리는 시간이다.
우리는 주어진 노드 k에서 신호를 보낼 것이다. n개의 모든 노드가 신호를 수신하는 데 걸리는 최소 시간을 반환하라. n개의 노드가 모두 신호를 수신할 수 없는 경우 -1을 반환한다.
다익스트라 풀이
원래 처음에는 <climits> 헤더를 포함해서 거리 벡터의 초기값을 INT_MAX로 두고 제출했었는데, 이전 거리와 새 거리를 비교하여 업데이트하는 부분에서 int 오버플로우가 나서 문제에서 주어진 범위에 맞춰 충분히 큰 숫자로 바꿨다. 100 * 100 * 10은 정점 수 * 가중치 최댓값 * 여분의 10이다.
정의된 함수의 앞부분부터 while까지는 다익스트라 알고리즘의 과정을 그대로 따르고, 마지막엔 알고리즘으로 찾은 거리 중 최댓값을 찾아 반환한다. 이때 찾아낸 최댓값이 거리 벡터를 초기화할 때 입력한 값과 같다면 연결되지 않은 정점이 존재하는 것이므로 -1을 반환하게 한다.
정점의 번호가 1부터 시작한다는 점에 주의해야 한다. 벡터나 배열의 인덱스가 0부터 시작하기 때문에 0번 인덱스는 사용하지 않는 값임을 명확히 하고, 이후 최댓값을 찾는 과정에서도 답으로 고려되지 않도록 해야 한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <vector>
// #include <climits>
using namespace std;
struct cmp { // 다익스트라 우선순위 큐 비교 연산자 : 가중치가 적고 정점 번호가 적은 것을 우선으로 함
bool operator()(pair<int, int> a, pair<int, int> b) {
if (a.second == b.second)
return a.first >= b.first;
else
return a.second > b.second;
}
};
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// times는 간선들, n은 정점 개수, k는 시작점
// dijkstra solution
int from, to, w, vert; // w는 가중치, vert는 매번의 반복마다 방문하는 정점
int max_w = INT_MIN; // 최댓값을 구해야 하기 때문에 최대한 작은 값으로 초기화
vector<int> dist(n + 1, 100 * 100 * 10); // 정점 번호가 1부터 시작하는 거리 벡터
vector<bool> visited(n + 1, false); // 방문 여부 초기화
priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> next_visit; // 다음에 방문할 정점 : (정점, 거리)
vert = k; // 이제 방문할 정점 : 아직 시작하지 않았으므로 시작점으로 초기화
visited[0] = true; // 안 쓰는 인덱스 방문할 일 없게 미리 표시
dist[k] = 0; // 시작점은 거리 0
dist[0] = INT_MIN; // 안 쓰는 정점 표시
next_visit.push(make_pair(k, dist[k])); // 시작점을 큐에 넣고 시작해야 반복문이 시작할 수 있다
// 1. 시작점 방문
// 2. 거리 파악
// 3. 가장 가까운 곳으로 이동
// 4. 반복
while (true) {
if (!visited[vert]) { // 이제 새로 방문하는 정점에 대해서만 수행 : 방문 표시를 중복하여 하지 않게 한다
visited[vert] = true; // 정점 방문
for (int x = 0; x < times.size(); x++) {
from = times[x][0];
to = times[x][1];
w = times[x][2];
if (from != vert) // 지금 방문한 정점에서 출발하는 간선이 아니면 계산하지 않는다
continue;
if (dist[vert] + w < dist[to]) { // 거리를 업데이트할 필요가 있을 때에만
dist[to] = dist[vert] + w; // 거리 업데이트
next_visit.push(make_pair(to, dist[to])); // 다음 방문 정점 큐에 추가
}
}
}
if (!next_visit.empty()) { // 비어있는데 꺼내면 오류 난다
// 모든 정점을 다 방문하고 나서도 큐가 빌 때까지 pop하기 때문에 오류 방지 필요
pair<int, int> next = next_visit.top(); // (정점, 거리)
next_visit.pop(); // pop 안 하면 무한반복으로 프로그램이 끝나지 않는다 : 자주 이거 빼먹어서 메모함
vert = next.first;
}
else // 다음 방문 정점 큐가 비어있다면 종료
break;
}
for (auto& i : dist) // 계산한 거리 중 최댓값 찾기
max_w = i > max_w ? i : max_w;
if (max_w == 100 * 100 * 10) // 찾은 최댓값이 처음에 설정한 초기값과 같다면 연결되지 않거나 경로가 없는 정점이 있음
return -1;
return max_w;
}
};

벨만-포드 풀이
거리 벡터의 초기화 값은 위의 다익스트라 풀이에서 설명한 대로 주어진 범위에 맞춰 충분히 큰 값으로 정했다. 다익스트라 풀이와 달리 함수의 앞부분에서 정의해둬야 할 값은 거리 벡터 이외에는 딱히 없다. 내가 느끼기엔 다익스트라로 쓰는 것보다 쉬웠다.
정점이 1번부터 시작해 n번까지 있으므로 (정점 수 - 1)만큼 반복하려면 1부터 n 미만까지 반복하는 반복문을 쓰면 된다. 그리고 내부에는 모든 정점에 대해 반복하는 반복문을 쓴다. 안쪽 반복문에서 각 간선과 해당 간선이 거치는 정점들에 대해 거리를 업데이트한다. 이렇게 한 번의 순회가 끝나면 음수 사이클을 찾기 위해 아래에서 동일한 과정을 한 번 더 하는데, 이 문제는 음수 가중치가 주어지지 않으므로 정답을 맞히기만 하는 데에는 딱히 필요 없는 과정이긴 하다. 음수 사이클 확인 과정을 빼고 제출하면 실행 시간이 절반 정도로 줄어든다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <vector>
// #include <climits>
using namespace std;
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// times는 간선들, n은 정점 개수, k는 시작점
// bellman solution
int from, to, w; // w는 가중치, vert는 매번의 반복마다 방문하는 정점
int max_w = INT_MIN; // 최댓값을 구해야 하기 때문에 최대한 작은 값으로 초기화
vector<int> dist(n + 1, 100 * 100 * 10); // 정점 번호가 1부터 시작하는 거리 벡터
dist[k] = 0; // 시작점은 거리 0
dist[0] = INT_MIN; // 안 쓰는 정점 표시
// 최단거리 구하기
for (int i = 1; i < n; i++) { // (정점 수 - 1)만큼 반복
for (int x = 0; x < times.size(); x++) { // 모든 간선에 대해 수행
from = times[x][0];
to = times[x][1];
w = times[x][2];
// 항상 최선의 값으로 업데이트한다
dist[to] = dist[to] > dist[from] + w ? dist[from] + w : dist[to];
}
}
// 음수 사이클 확인 : 없어도 정답 통과 가능
for (int i = 1; i < n; i++) {
for (int x = 0; x < times.size(); x++) {
from = times[x][0];
to = times[x][1];
w = times[x][2];
// 같은 과정을 수행해서 업데이트가 생기면 음수 사이클 존재
if (dist[to] > dist[from] + w)
return -1;
}
}
for (auto& i : dist) // 계산한 거리 중 최댓값 찾기
max_w = i > max_w ? i : max_w;
if (max_w == 100 * 100 * 10) // 찾은 거리 중 초기값이 있다면 경로가 없는 정점이 있음
return -1;
return max_w;
}
};


