2580 스도쿠 미해결로 인해 풀이 대신 공부함
문제 참고(출처 : 백준)
15649 N과 M (1), 15650 N과 M (2), 15651 N과 M (3), 15652 N과 M (4)
9663 N-Queen, 2580 스도쿠
목차
- 재귀와 호출 스택
- 깊이 우선 탐색
- 백트래킹
재귀와 호출 스택
가볍게 “재귀”의 정의부터 읽어보고 시작하자. 출처는 네이버 사전이다.
재귀 再歸
- 원래의 자리로 되돌아가거나 되돌아옴.
- 주어진 문제를 해결하기 위하여 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 방식. 어떤 루틴이나 프러시저가 자기 자신을 반복적으로 호출하여 문제를 풀어 나가는 알고리즘으로, 이를 이용하기 위해서는 스택을 사용한다. 간단한 루틴을 풀 수 있지만, 처리 속도가 느리고 횟수가 지나치게 많으면 프로그램이 정지하기도 한다.
예상치 못하게 내가 할 설명을 네이버에게 뺏겼다. 하지만 저 말도 괜히 있어보이고 어렵게 생겼으니 내 특기인 없어보이지만 이해는 되는 말로 다시 설명하겠다.
재귀, 또는 재귀 함수라고 해도 된다. 함수가 자기 자신 내에서 스스로를 다시 호출하면 그것을 재귀 함수라고 부른다. 가볍게 활용해볼만한 예시로는 팩토리얼, 피보나치 수 등이 있다. 사람의 말로 길게 설명하는 것보다 예시 하나 보고 한 줄 한 줄 뜯어보는 게 훨씬 이해가 빠를 테니 내가 쓴 코드부터 보자.
문제 참고 : 백준 10872 팩토리얼
깃허브 : C++ 소스 코드
사용 언어 : C++ (파이썬과 자바는 아직 추가 계획이 없다)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
using namespace std;
int fac(int n); // 팩토리얼 함수
int main()
{
int n;
cin >> n;
cout << fac(n);
return 0;
}
int fac(int n)
{
if (n <= 1) // n이 1보다 작거나 같다면 1을 반환한다. n이 0일 때도 포함한다, 0! = 1이다.
return 1;
else // n이 1보다 크다면 1이 될 때까지 (n - 1)로 다시 함수를 호출한다.
return n * fac(n - 1);
}
main() 부분에서는 딱히 볼 것이 없다. 입력을 받고 함수를 호출해 반환된 값을 출력하는 것뿐이다. 봐야 할 것은 함수에 쓰인 코드이다.
함수 내부는 크게 둘로 나뉜다. 인자로 전달된 n이 1 이하인 경우와 1을 초과하는 경우.
(1) n이 1 이하인 경우
이 함수의 의미는 전달받은 정수의 팩토리얼 값을 계산하는 것이기 때문에 그 숫자가 0이거나 1이라면 계산할 필요가 없다. 어차피 답은 1이고 새삼스럽게 더 곱한다고 뭔가 대단한 1이 되지도 않는다.
(2) n이 1을 초과하는 경우 == n이 1보다 큰 경우
(1)의 경우와 달리 곱해야 할 수가 있는 상황이다. 하지만 지금 받은 수는 n 하나뿐이다. 이때 반복문을 쓰지 않고 할 수 있는 것이 재귀 호출이다. n을 알았다면 n보다 1 작은 수도 알 수 있다. 그러면 (n - 1)의 팩토리얼 값에 n을 곱하면 n!의 값을 알 수 있다. 다시 말해 n은 마지막에 숟가락만 얹을 테니 나머지 계산은 (n - 1)에게 미룬다는 것이다. n은 (n - 1)에게 계산을 미루고, 그 (n - 1)은 다음 호출에서 다시 n이 되어 또다른 (n - 1)에게 계산을 미룬다. 이 폭탄 돌리기의 현장에서 실제로 의미있는 값을 반환할 줄 아는 건 0과 1밖에 없다. 그러므로 재귀 호출은 n이 1보다 작거나 같아질 때까지 이어진다. 나는 이 값(1 또는 0)을 반환점이라고 부른다. 실제로 학계에서 의미가 있는 말인지는 모르겠다만, 내 편의상 그렇게 부르고 있다.
내가 1을 반환점이라고 부르는 것은 이유가 있다. 지금까지 빚처럼 쌓여만 오던 함수 호출을 청산하기 시작하는 지점이기 때문이다. 계속 n이라고만 하면 헷갈리니까 가볍게 4!을 구한다고 생각하고 그 과정을 따라가 보자.
- 먼저 사용자는 4!의 값을 받기 위해 fac(4)를 호출한다.
- 함수 내부에서 4는 1보다 크기 때문에 else로 넘어가 4 * fac(3)을 반환한다. 이때 fac(3)의 값은 모르는 상태이기 때문에 프로그램은 결과를 반환하기 전에 fac(3)를 호출한다.
- fac(3)가 호출되었기 때문에 이번에도 else로 넘어간다. fac(3)은 3 * fac(2)를 반환하고 싶다. 하지만 fac(2)의 값을 모른다. 그러니 다시 호출한다.
- fac(2)는 2 * fac(1)을 반환하고 싶다. 하지만 fac(2)는 fac(1)의 값을 모른다. 재차 호출한다.
- fac(1)은 자신의 값을 안다. 1을 반환한다.
- 방금 호출이 왔던 2 * fac(1)로 돌아간다. 값을 알아냈으니 2 * 1인 2를 반환한다.
- 3 * fac(2)로 돌아간다. 3 * 2인 6을 반환한다.
- 4 * fac(3)으로 돌아간다. 4 * 6인 24를 반환한다. 이 값은 사용자에게 전달된다.
줄줄이 이어지는 함수 호출은 n이 1이 되어서야 끝을 맺고 지금껏 지나온 모든 호출들을 청산했다. 이 과정까지는 이제 무슨 말인지 알 수 있다. 하지만 의문이 남는다. 함수가 한 차례 끝나기도 전에 다시 호출하면 이전의 값들은 어떻게 알고 그 값을 그대로 되돌려주는가?
혹시 모르니 스택에 대해 잠깐 알아보고 가자. 이 글의 주요 개념은 아니니 깊이 알 건 없고, 프링글스 통이라고 생각하면 된다. 감자칩이 약간의 틈을 두고 켜켜이 쌓인 프링글스 통의 과자를 먹으려면 위에서부터 하나씩 집어먹어야 한다. 맨 아래에 있는 과자를 먼저 꺼내먹으라고 만든 구조는 당연히 아니다. 스택도 이와 비슷하다. 어떤 값들이 차례로 저장되어 들어오고, 사용자는 필요할 때 그것을 다시 꺼내 쓴다. 이때 마지막으로 들어온 데이터가 가장 먼저 꺼내진다. 지금 알아야 할 스택의 개념은 이 정도면 됐다. 앞으로 설명할 호출 스택이란 프로그램을 실행하면서 쌓인 함수 호출 등을 저장하는 스택인 것이다.
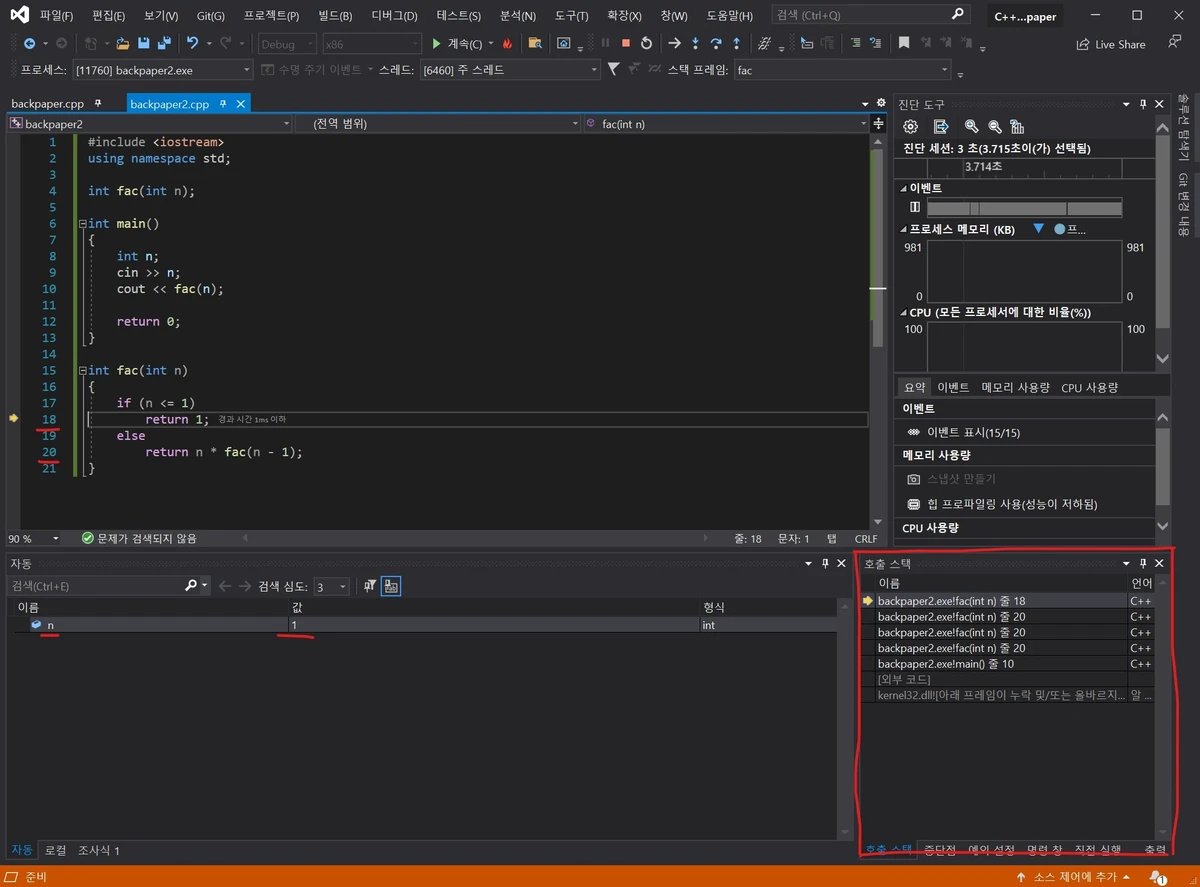
(이 문단의 내용은 내가 어떠한 자료를 참고하여 공부한 것이 아니고 디버깅 중 호출 스택을 보며 알아낸 것이기 때문에 부족하거나 부적절한 내용이 있을 수 있다. 만약 있다면 알려주길 바란다.) 함수의 호출은 우리가 생각하는 것처럼 단편적이거나 평면적인 과정이 아니다. 모든 완료되지 않은 호출은 ‘호출 스택’이라는 것에 저장된다. 컴파일러마다 화면이 다르니 정확히 어디서 확인할 수 있는지는 알려줄 수 없다. 대신 내가 쓰는 비주얼 스튜디오 화면[이미지 1]을 보여줄 테니 참고하자. 캡쳐한 시점은 입력 값으로 4를 입력해 fac(4)가 호출되고 재귀를 거쳐 fac(1)에서 1이 반환되기 직전이다. 빨간 선으로 조금 구겨진 네모가 쳐진 곳이 호출 스택이 나타나는 부분이다. 호출 스택에 보이는 것은 호출이 온 줄의 번호 뿐이지만 호출된 순간의 변수 상태도 같이 저장된다. 그렇기 때문에 함수 내에서 자기 자신을 재차 호출해도 앞선 호출에 저장된 값을 덮어쓰지 않는다. 나는 이걸 몰라서 재귀함수에 대해 한참을 이해하지 못하고 있었다.
- 깊이 우선 탐색
백트래킹에 대해 배우려면 먼저 깊이 우선 탐색이라는 것을 알아야 한다. 이것도 개념만 놓고 본다면 그리 어렵지 않다. 가볍게 ‘탐색’에 대해서부터 알아보자. 어떠한 알고리즘을 이용해 원하는 값을 찾는 것과 그 방법 등을 크게 일러 탐색이라고 한다. 그 종류는 꽤나 다양한데 단순히 원하는 값이 나올 때까지 모든 값을 하나씩 까보는 방법도 있고, 여러 갈래로 갈라지는 분기를 하나씩 들러 찾아보는 방법도 있다. 이중 깊이 우선 탐색은 여러 갈래로 갈라지는 분기를 앞에서부터 하나씩, 끝까지 가보고 원하는 값인지 아닌지 판단하는 방법이다. 자매품으로 너비 우선 탐색이 있는데, 이 방법은 갈 수 있는 분기를 모두 하나씩 들러보면서 내려간다. 둘 모두 주로 트리나 그래프라는 자료구조에서 활용한다. 그래프라는 것은 수학에서 사용하는 x 축과 y 축이 있는 그것은 아니고, 쾨니히스베르크의 다리를 검색하면 나오는 이미지 같은 것을 말한다.
깊이 우선 탐색에 대해 조금 더 알아보자. 한빛 아카데미 출판, <소프트웨어 세상을 여는 컴퓨터 과학>에 의하면 깊이 우선 탐색은 “시작 정점에서 시작하여 그 정점과 연결된 방문하지 않은 한 정점을 방문하고, 다음에는 방문한 정점에서 다시 연결된 방문하지 않은 한 정점 순으로 방문한다. 진행하다가 더 이상 진행할 수 없으면 왔던 길을 되돌아가면서 아직 방문하지 않은 한 정점을 방문한다.”라고 한다.
예를 들어 보자. 여기 1부터 3까지의 자연수가 있다. 사용자는 중복 없이 사전 순으로 이 수들을 두 개씩 뽑아 짝을 짓고 싶다. 이때 사용할 수 있는 방법이 깊이 우선 탐색이고, 여기에 백트래킹도 포함된다. 일단은 깊이 우선 탐색만 생각해보자.
- 가장 먼저 1을 하나 뽑는다.
- 1의 짝으로 올 수 있는 숫자는 2, 3이 있다. 먼저 2를 뽑아 하나의 짝을 완성한다. → (1, 2)
- 다시 1을 하나 뽑는다.
- 이번에 1의 짝으로 올 수 있는 숫자는 3뿐이다. → (1, 3)
- 1로 만들 수 있는 짝은 다 만들었으니 이번에는 2를 뽑는다.
- 2의 짝으로 올 수 있는 숫자는 1과 3이다. 1을 먼저 뽑는다. → (2, 1)
- 이후의 과정은 생략한다. → (2, 3), (3, 1), (3, 2)
간단하고 빠른 설명을 위해 소박한 예시를 들어 깊이라는 말이 잘 체감되지 않을 수 있다. 좀 더 예시가 필요하다면 위의 예시에서 숫자를 더 크게 잡아보거나 스스로 그럴싸한 예시를 고민해 보자. 직접 문제를 만들어보는 것도 공부에 도움된다.
- 백트래킹
백트래킹은 깊이 우선 탐색의 개정판 같은 것이다. 앞서 알아본 깊이 우선 탐색은 답을 찾기 위해 전진만 할 줄 알았지, 지금 가는 길이 답이 아니라는 것을 알았을 때 되돌아갈 줄은 몰랐다. 백트래킹은 깊이 우선 탐색이 뒷걸음질을 치게 만드는 알고리즘이다. 참고할만한 문제는 글의 서두에 적어두었으니 다른 사람의 풀이를 찾아봐도 좋고 혼자 도전해도 좋으니 한번 풀어보자. 나도 보고 배웠으니 여기서 풀이할 마음 없다.
비교하기 좋게 예시를 재활용하자. 숫자가 너무 적으면 결과도 적으니 이번엔 1부터 4까지의 자연수를 중복 없이, 오름차순으로 2개씩 뽑아보겠다. 당연히 사전순으로 뽑는다.
- 1을 뽑는다.
- 1의 짝으로 올 수 있는 수는 2, 3, 4이다. 2를 먼저 뽑는다. → (1, 2)
- 뽑았던 2를 도로 내려놓고 다른 수를 뽑는다. 남은 것은 3과 4이니 3을 뽑는다. → (1, 3)
- 3을 도로 내려놓고 다른 수를 뽑는다. 4가 남았다. → (1, 4)
- 4를 내려놓고 나니 1의 짝으로 남은 수가 없다. 1도 내려놓는다.
- 1은 끝났으니 2를 뽑는다.
- 1은 2보다 작으니 치워놓고, 2의 짝으로 가능한 수는 3, 4이다. 3을 뽑는다. → (2, 3)
- 3을 내려놓고 남은 수는 4이다. → (2, 4)
- 4를 내려놓고 나면 남은 수가 없다. 2도 내려놓는다.
- 이하 생략 → (3, 4)
이 알고리즘에서 핵심적인 역할을 하는 것이 재귀 호출이다. 숫자 하나를 뽑아 놓은 상태에서 숫자를 뽑는 함수를 재차 호출해 다음 수를 뽑는다. 뽑기가 끝나면 결과를 출력하고 뽑은 수를 돌려놓는다. 호출이 끝나 돌아올 때는 해당 줄로 똑같이 되돌아와서 그 다음 줄을 바로 실행하기 때문에 재귀 호출이 있는 부분 위에서는 수를 뽑고, 재귀 호출 아래에서 뽑은 수를 돌려놓는 코드를 쓰면 위와 같은 과정이 가능하다. 문제를 풀이할 생각은 없다고 했지만 아무래도 예시가 없으면 아쉬우니 조금만 보자. 15650 N과 M (2) 문제에 사용한 함수이다.
사용 언어 : C++, 파이썬
파이썬 코드 : [파이썬 소스 코드]
[C++ 소스 코드 일부]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void pr(int n, int m) // n개의 수 중에서 중복 없이 오름차순으로 m개의 수를 뽑음
{
if (v.size() == m) // 필요한 만큼 수를 뽑았을 때 실행
{
// 뽑은 수를 출력한다.
for (int i = 0; i < v.size(); i++)
cout << v[i] << " ";
cout << "\n";
return; // 실행이 끝나고 이전 호출로 되돌아간다.
}
// 아직 수를 충분히 뽑지 못했을 때
for (int i = 0; i < n; i++) // 숫자의 총 개수만큼 반복 : 첫 번째 숫자부터 끝까지 하나씩 조건에 맞는지 시도해본다
{
if (nvi[i] || (i + 1) < idx) // 이미 뽑은 숫자이거나 직전에 뽑은 숫자보다 작은 숫자일 경우
continue; // 숫자를 뽑지 않고 넘긴다
v.push_back(i + 1); // 넘기지 않았다면 숫자를 뽑는다.
idx = i + 1; // 오름차순으로 하기 위해 지금 뽑은 숫자를 기록한다.
nvi[i] = 1; // 중복 방지를 위해 뽑았다는 것도 표시해 둔다.
pr(n, m); // 재귀 호출
v.pop_back(); // 호출에서 되돌아왔을 때 실행한다. 뽑은 숫자를 하나 버린다.
idx = 0; // 기록한 숫자를 지운다.
nvi[i] = 0; // 뽑았다는 표시도 지운다.
}
}
내가 이 알고리즘이 어려웠던 이유는 재귀호출 이후 되돌아올 때 이전의 변수 상태까지 같이 되돌아간다는 것을 알지 못했기 때문이었다. 지금은 그건 알지만 그냥 문제가 어렵다.. 이론을 아는 것과 활용이 되는 건 꽤 다른 문제다.
숫자 뽑기 예시에서는 뽑아둔 숫자를 다 사용한 후 다시 버리기 위해 재귀 호출 뒤의 코드에 숫자를 지우는 부분이 들어갔지만 굳이 그런 과정이 필요 없는 경우에는 return;을 쓰기도 한다. 그리고 재귀를 설명할 때 내가 “반환점”을 언급한 적이 있는데, 꼭 모든 재귀 함수와 백트래킹이 반환점을 돌아서 가지는 않는다. 일례로 9663 N-Queen 문제는 함수에 전달하는 첫 인자로 0을 넘긴다고 풀이한다. n에서부터 0까지 가는 과정이 필요하지 않기 때문에 하지 않는 것이라고 본다. 2580 스도쿠 문제도 비슷하게 시작하지만, 아직까지는 그 풀이를 이해하지 못하기도 했고, 내가 쓴 풀이에 미련이 남아 더이상 진행할 수가 없다. 내 풀이를 잊을 때까지 시간이 좀 필요하다..
참고 도서
<소프트웨어 세상을 여는 컴퓨터 과학>, 김종훈 지음, 한빛 아카데미 출판
