과제
아래 내용을 포함하는 포트폴리오를 작성하고, 웹페이지 주소를 제출합니다.
1. Data structures augmentation 코딩
- Rank 구현
- AVL tree 구현
2. AVL tree 정의 등 강의 내용 정리
*Geeks for geeks 참조하세요.
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
3. Leet code 문제 풀이
https://leetcode.com/problems/balanced-binary-tree/
목차
- 균형 이진 트리
- AVL 트리
- 삽입과 삭제
- 회전 유형
- LL 타입
- RR 타입
- RL 타입
- LR 타입
관련 글
균형 이진 트리
* 이 글은 [자료구조] 이진 탐색 트리 Rank에서 이어지는 글이며, 독자가 이진 탐색 트리에 대해 알고 있음을 전제로 한다. 이진 탐색 트리의 개념에 대한 글은 여기에서 볼 수 있다.
보통 이진 탐색 트리는 탐색 연산의 시간 복잡도를 O(logn)으로 간주하며, 그것이 최선이다. 그러나 모든 이진 탐색 트리가 최선을 보장하지는 못한다. 예를 들어 정렬된 배열이 순서대로 이진 탐색 트리에 입력되었다고 해보자. 최선을 보장하지 못하는 이진 탐색 트리는 첫 번째 요소를 루트로 하고 다음으로 입력되는 모든 값을 적절한 자리에 넣을 것이다. 결과적으로 그 트리의 모양은 배열과 다를 바 없게 된다. 그러므로 이 트리는 O(n)의 시간 복잡도를 갖는다.
항상 그랬듯이 내가 문제점을 설명하는 건 다 해결하기 위해서다. 어떻게 할 수 있을까? 답은 이 본문의 소제목에 있다. 배열처럼 곧게 뻗은 트리를 구부려 트리처럼 만들어주면 된다. 그것이 균형 트리이고, 지금은 이진 트리에 대해서만 공부하고 있기 때문에 균형 이진 트리이다.
내가 공부하는 교재[1]의 설명에 따르면 균형 트리를 만드는 방법은 아주 다양하고 복잡하다고 한다. 그렇기 때문에 책에서는 AVL 트리에 대해서만 설명하였고, 지금은 나도 그에 대해서만 공부할 것이다.
AVL 트리
AVL 트리는 Adelson-Velskii와 Landis에 의해 제안된 트리로 각 노드에서 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 1 이하인 이진 탐색 트리를 말한다.[1]
AVL 트리의 정의는 간단하게 책에 써있는 것을 그대로 인용했다. AVL 트리는 저 균형을 유지하기 위해 트리의 균형이 깨지는 순간 노드를 재배치해 다시 균형 상태로 만든다. 그렇게 함으로써 O(logn)의 연산 시간을 보장한다. 탐색 연산은 이진 탐색 트리와 같고, 바꾸어야 할 것은 삽입과 삭제 연산이다.
삽입과 삭제 연산을 설명하기에 앞서, 트리의 높이에 대해 정의해야 한다. AVL 트리에서 말하는 높이란, 어떤 노드에 대하여 그 노드에서 찾아갈 수 있는 가장 낮은 리프노드까지의 높이 차를 말한다. 리프노드는 자신이 리프노드이기 때문에 높이가 0이고, 리프노드의 부모 노드는 1, 그 위의 노드는 2가 되는 방식이다. 트리 전체의 레벨 수를 의미하는 높이와는 다르다. 그리고 AVL 트리의 양쪽 서브트리 높이 차이는 균형 인수라고 부른다.
삽입과 삭제
AVL 트리에 새 요소를 삽입할 때는 통상의 트리 삽입과 같은 연산을 수행한다. 이후 새 요소의 부모 노드의 높이를 업데이트하고 균형을 검사하는 것이다. 새 노드 위의 부모 노드의 균형 상태에 따라 수행할 회전 연산이 결정된다.
삭제 연산도 삽입 연산과 마찬가지로 삭제를 한 후에 균형을 바로잡는다. 이때도 부모 노드의 높이를 업데이트하고 균형을 검사하며, 회전 연산의 유형 결정 방식은 삽입 연산과 동일하다.
삽입 및 삭제의 과정은 참고자료 [2], [3]을 참고하여 서술했다.
회전 연산
AVL 트리에서 사용하는 회전 연산은 네 가지 유형이 있고, 특정 노드의 균형 인수가 ±2일 때 회전 연산을 수행한다. 아래 문단에 첨부된 모든 회전 유형 이미지의 출처는 참고자료 [1]이다.
LL 타입
왼쪽으로만 자식이 이어지는 형태로 균형이 깨졌을 때 사용한다. 예를 들어 6 → 5 → 2 순서로 노드가 삽입된 경우가 이에 해당하고, 이를 일반화하면 어떤 조상 노드의 왼쪽 서브트리의 왼쪽 서브트리에 자식이 추가된 상황이다. 해당 조상 노드가 그 왼쪽 서브트리의 오른쪽 자식이 되도록 바꾸어 해결할 수 있다. 그림으로 보면 아래와 같다.
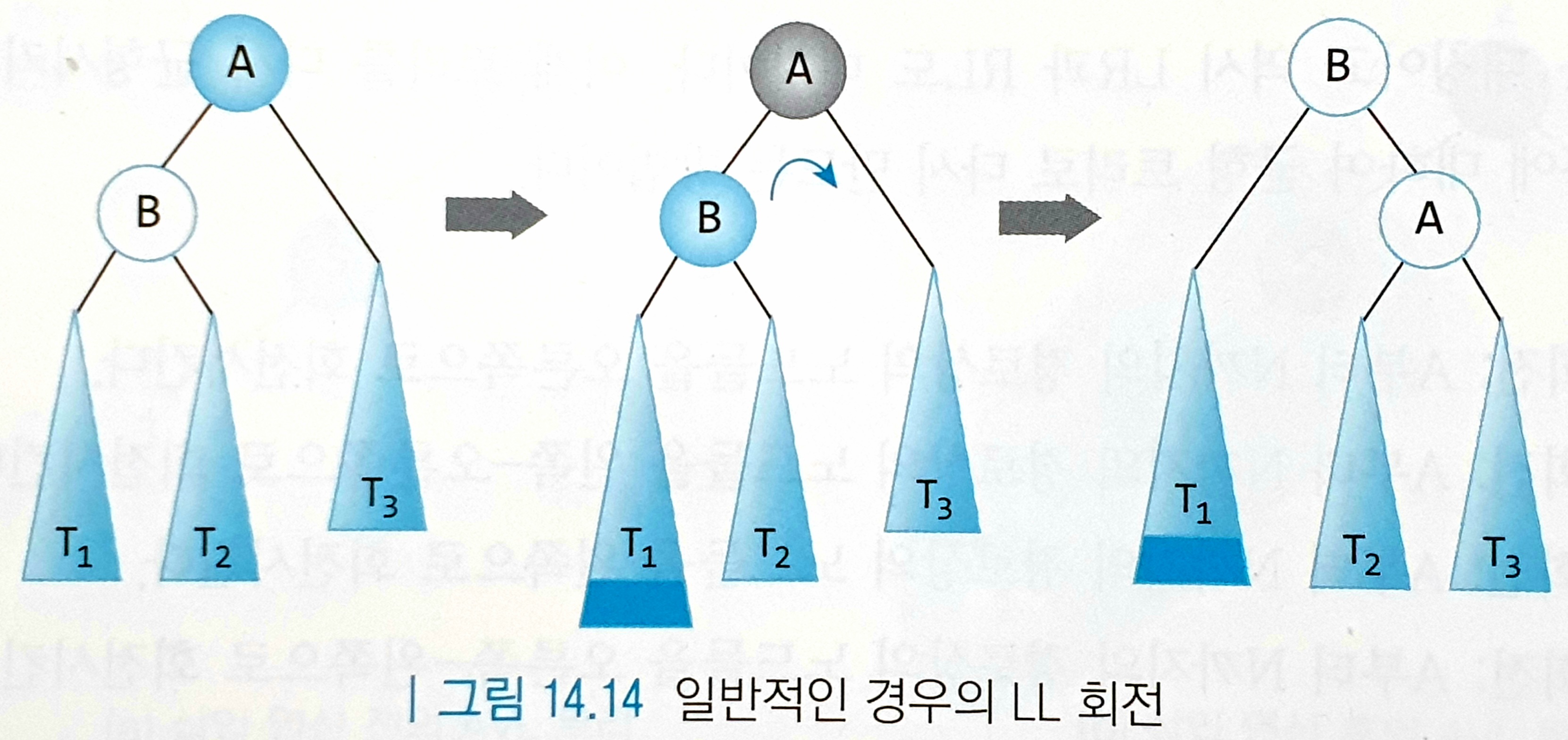
프로그램으로 구현할 때는 다음과 같은 알고리즘으로 한다.
1
2
3
4
rotate_LL(A)
B ← A의 왼쪽 자식
B의 오른쪽 자식을 A의 왼쪽 자식으로 만든다.
A를 B의 오른쪽 자식 노드로 만든다.
RR 타입
LL 타입과 반대로 오른쪽 서브트리가 오른쪽으로 길어지는 경우이다. 해결할 때에도 LL 타입과 반대 방향으로 회전하면 된다. 그림으로 보면 아래와 같다.
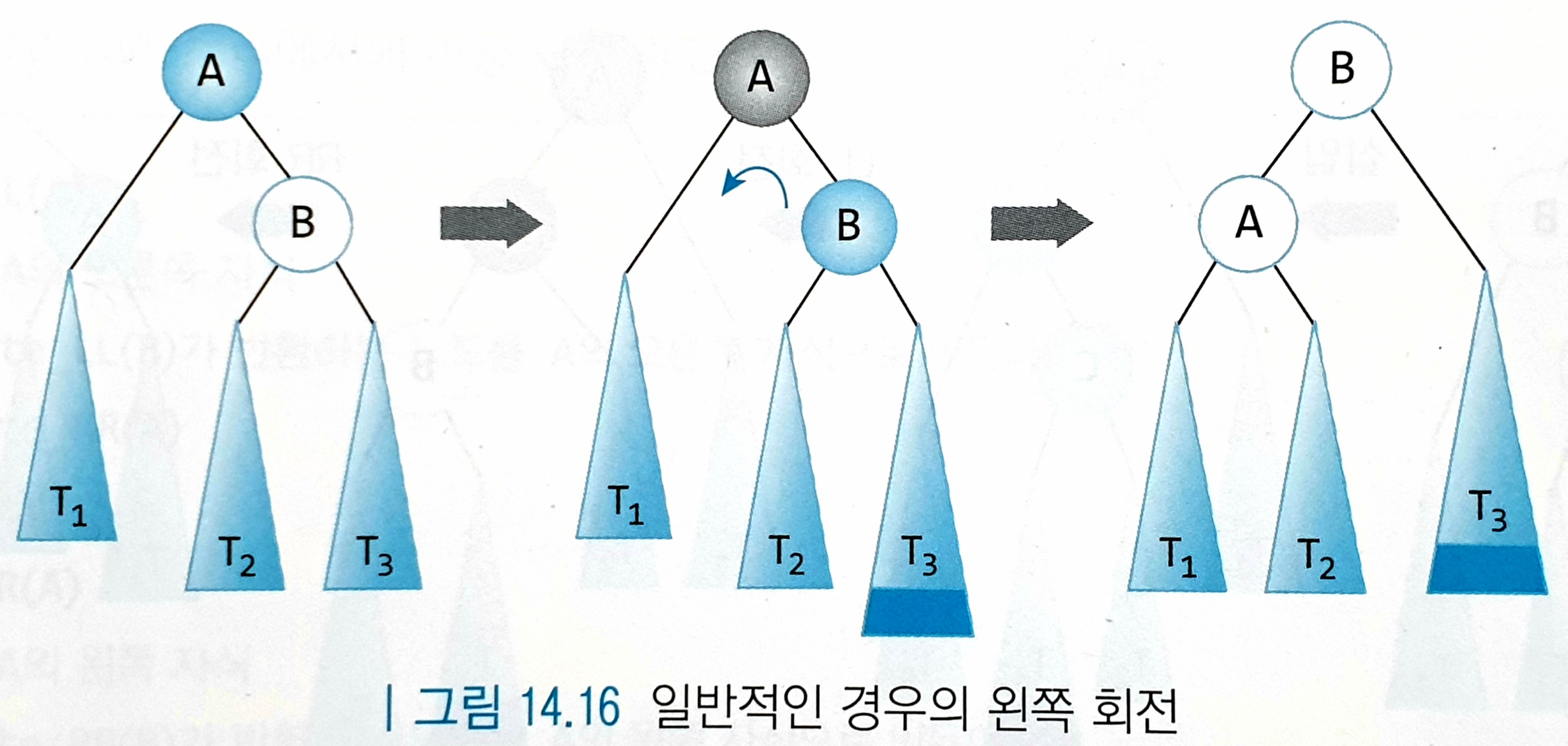
프로그램으로 구현할 때는 다음과 같은 알고리즘으로 한다.
1
2
3
4
rotate_RR(A)
B ← A의 오른쪽 자식
B의 왼쪽 자식을 A의 오른쪽 자식으로 만든다.
A를 B의 왼쪽 자식 노드로 만든다.
RL 타입
어떤 노드의 오른쪽 서브트리의 왼쪽 서브트리에 새 노드가 추가되어 균형이 깨지는 경우이다. 이 경우 LL 회전을 한 후 RR 회전을 하면 된다. 그림으로 보면 아래와 같다.
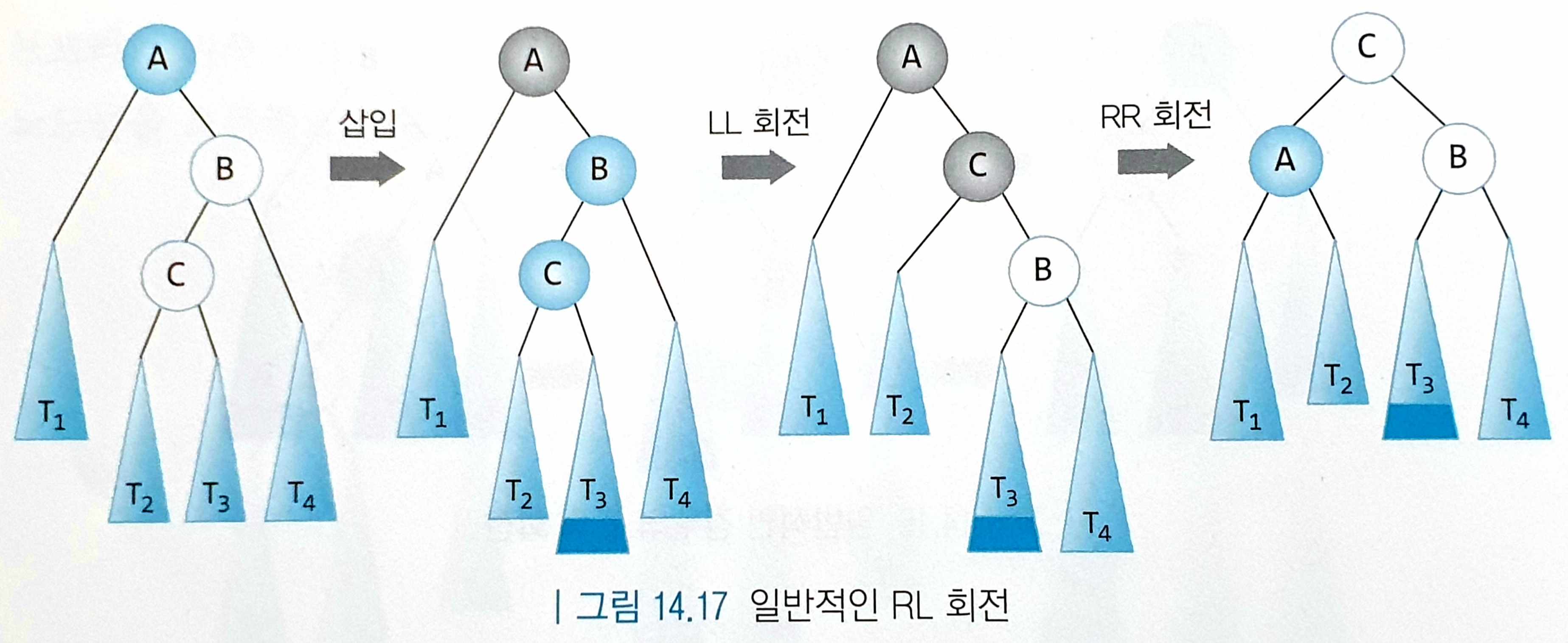
프로그램으로 구현할 때는 다음과 같은 알고리즘으로 한다.
1
2
3
4
rotate_RL(A)
B ← A의 오른쪽 자식
rotate_LL(B)가 반환하는 노드를 A의 오른쪽 자식으로 만든다.
rotate_RR(A)
LR 타입
어떤 노드의 왼쪽 서브트리의 오른쪽 서브트리에 새 노드가 추가되어 균형이 깨지는 경우이다. RL 타입과 반대로 RR 회전을 한 후 LL 회전을 하면 된다.
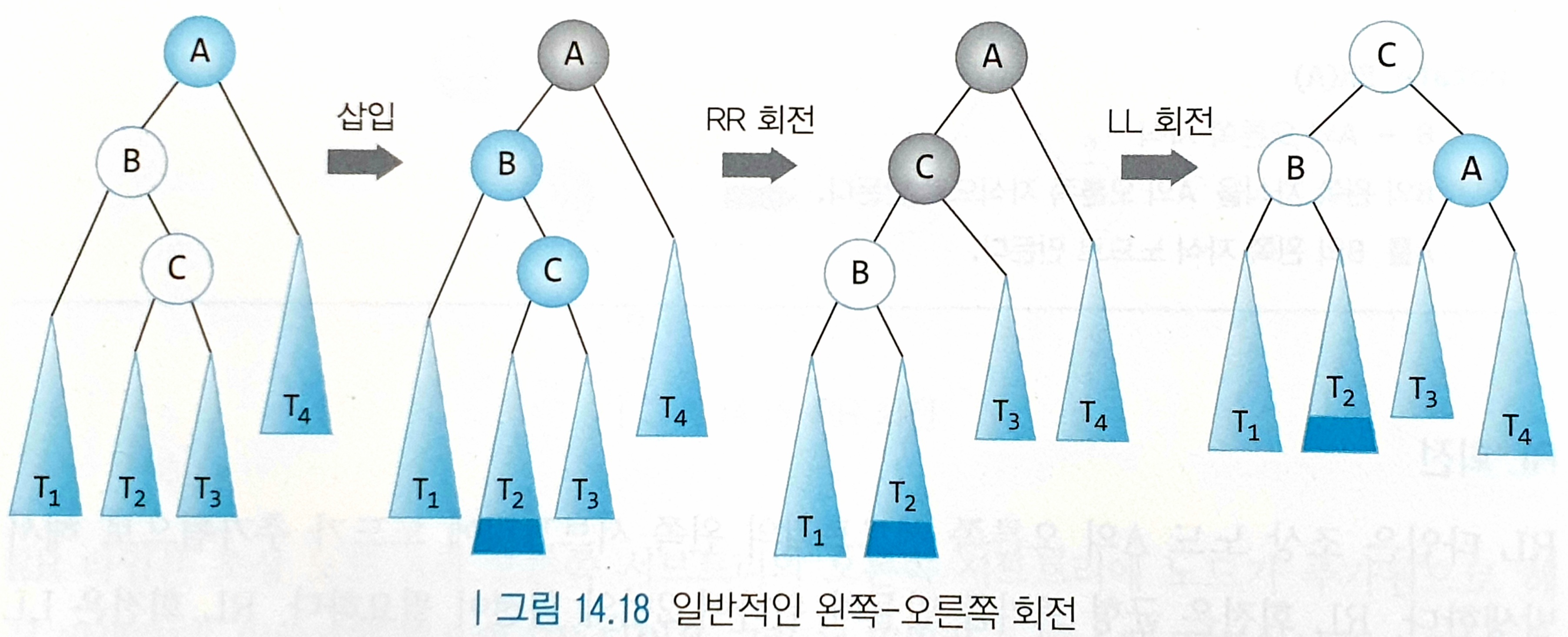
프로그램으로 구현할 때는 다음과 같은 알고리즘으로 한다.
1
2
3
4
rotate_LR(A)
B ← A의 왼쪽 자식
rotate_RR(B)가 반환하는 노드를 A의 왼쪽 자식으로 만든다.
rotate_LL(A)
----------------------------------------------
혹시나 내가 글을 완성하지 못할 때를 대비해 써둡니다. 코로나 의심 증상이 있어서 검사도 받고 하루 쉬느라 글을 완성하지 못했습니다. 이상 변명 끝.
추가 설명 : 확진됐음
참고 자료
[1] 『C++로 쉽게 풀어쓴 자료구조』, 천인국ㆍ최영규 지음, 생능 출판사
[2] AVL Tree | Set 1 (Insertion), https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
[3] AVL Tree | Set 2 (Deletion), https://www.geeksforgeeks.org/avl-tree-set-2-deletion/
