Table of Contents
할 일
- Read chapters 7.1 – 7.7. (X)
- Solve the exercise problem 14 of the chapter 7.
Show that the time complexity for the number of assignments of records for the Mergesort algorithm (Algorithms 2.2 and 2.4) is approximated by T (n) = 2n lg n.
- Refer to graph examples 1 and 2 on pages 21-22 of the class material titled ‘Class material 06.pdf’. Given the graph, perform a Bi-Directional Search. The source vertex is ‘s’, and the target vertex is ‘D’. Draw the graphs for each step of your procedure.
- Can you improve this Bi-Directional Search algorithm? Describe the procedure.
note. The third problem in the class material has been updated as described above.
- 7.1장~7.7장을 읽습니다. (X)
- 7장의 연습 문제 14를 풀어봅니다.
병합 정렬 알고리즘(알고리즘 2.2와 2.4)의 레코드 할당 횟수에 대한 시간 복잡도는 T(n) = 2n lg n으로 근사화됨을 나타냅니다.
- ‘Class material 06.pdf’의 21~22페이지에 있는 그래프 예제 1과 2를 참고합니다. 그래프가 주어지면 양방향 검색을 수행합니다. 시작점은 ‘s’이고, 도착점은 ‘D’입니다. 절차의 각 단계에 대한 그래프를 그립니다.
- 이 양방향 검색 알고리즘을 개선할 수 있습니까? 절차를 설명하세요.
참고. 수업 자료의 세 번째 문제는 위에서 설명한 대로 업데이트되었습니다.
문제 풀이
문제: 병합 정렬 알고리즘(알고리즘 2.2와 2.4)의 레코드 할당 횟수에 대한 시간 복잡도는 T(n) = 2n lg n으로 근사화됨을 나타냅니다.
문제 이해: 병합 정렬 수행 중 대입 연산 횟수가 2n log n으로 근사함을 증명해라. 편의상 n은 2의 거듭제곱으로 가정하겠다.
문제에서 말하는 병합 정렬 알고리즘은 두 가지이다. 하나는 배열을 반으로 나누어 다른 배열에 복사한 후 정렬하는 것이고, 다른 하나는 배열을 분할하는 과정을 배열의 인덱스를 이용해 복사하지 않고 진행하지만 병합을 할 때 새로운 배열에 저장한 후 정렬 결과를 원본에 붙여넣는 방식이다. 배열을 복사하는 순서가 다를 뿐, 원본을 복사해 넣을 새 배열이 필요하다는 점은 같다.
교수님이 시간복잡도 계산은 약간의 직관이 필요하다고 하셨으니 내가 한번 직관적으로 계산해 보겠다.
병합 정렬 알고리즘의 시간복잡도는 O(n log n)으로 알려져 있다. 이 시간복잡도는 (1) 계수가 생략되어 있고, (2) 분할/비교 등 알고리즘의 주요 연산에 대한 시간복잡도이다. 물론 연산에는 대입도 포함되어 있을 것이지만, 그것은 분할과 비교의 결과로써 수행되는 것이므로 전체 시간 복잡도를 바꿀 만큼 영향을 주기는 힘들다고 본다.
여기서 내가 생각해보는 것은 알고리즘이 수행되는 동안 비교 연산이 이루어지는 횟수이다. 분할은 그렇다 치고, 대입 연산은 비교 연산의 결과로 정렬이 이루어진 부분 배열에 대해 이루어지는 것이니(분할할 때부터 새 배열에 대입하는 알고리즘은 지금의 논리에서 순서만 바꾼 것이라고 가정한다.) 비교 연산과 대입 연산의 수행 횟수에는 서로 비례할 것이다.
그렇다면 병합 정렬 알고리즘에서 비교 연산은 얼마나 수행될까? 배열 분할을 모두 한 후의 시점부터 비교 연산을 시작하니 그것부터 따져보자.
| 부분 배열 크기 | 부분 배열 수 | 배열간 비교 횟수 | 총 대입 수 |
|---|---|---|---|
| 1 | n | 1 | 2 * n/2 |
| 2 | n/2 | 3 | 4 * n/4 |
| 4 | n/4 | 7 | 8 * n/8 |
| 2^k | n/2^k | 2^k * 2 - 1 | 2^k * 2 * n/2^(k+1) |
배열을 비교한 후 병합할 때 대입 횟수는 배열의 크기와 같다. 그리고 병합의 횟수는 배열을 분할한 수와 같다. 배열을 분할한 수는 log n이고, 비교 후 대입 수는 n이므로 총 비교 후 대입 수는 n log n이다. 또한 이는 배열을 분할하여 빈 배열에 대입할 때에도 똑같다. 그러므로 총 대입 연산 횟수는 2n log n이다.
양방향 다익스트라
문제: ‘Class material 06.pdf’의 21~22페이지에 있는 그래프 예제 1과 2를 참고합니다. 그래프가 주어지면 양방향 검색을 수행합니다. 시작점은 ‘s’이고, 도착점은 ‘D’입니다. 절차의 각 단계에 대한 그래프를 그립니다.
문제 이해: 강의자료의 지정된 페이지에는 D라는 레이블을 갖는 정점이 없다. (문제 좀 제대로 내달라고요) 대신 t가 도착점이라고 간주하고 두 그래프에 대해 양방향 다익스트라를 해보겠다.
양방향 다익스트라는 출발점과 도착점에서 동시에 출발하여 서로의 경로가 만났을 때 탐색을 종료하는 알고리즘이다. 길을 둘이서 같이 찾으니 혼자서 찾는 것보다 훨씬 빠르다고 한다.
사람이 이 문제를 풀기 위해서는 헷갈리지 않게 도착점에서 출발하는 그래프를 따로 그릴 필요가 있을 것 같아서 그래프를 2개 준비했다. 하나는 문제에서 준 그래프이고, 하나는 모든 간선의 방향을 뒤집은 반전 그래프이다. 가중치 중에 4 / 5라고 쓰인 것은 문제 그래프가 두 종류 있기 때문이다. 한 그래프는 w를 거치는 모든 간선의 가중치가 4이고, 다른 그래프는 5이다.
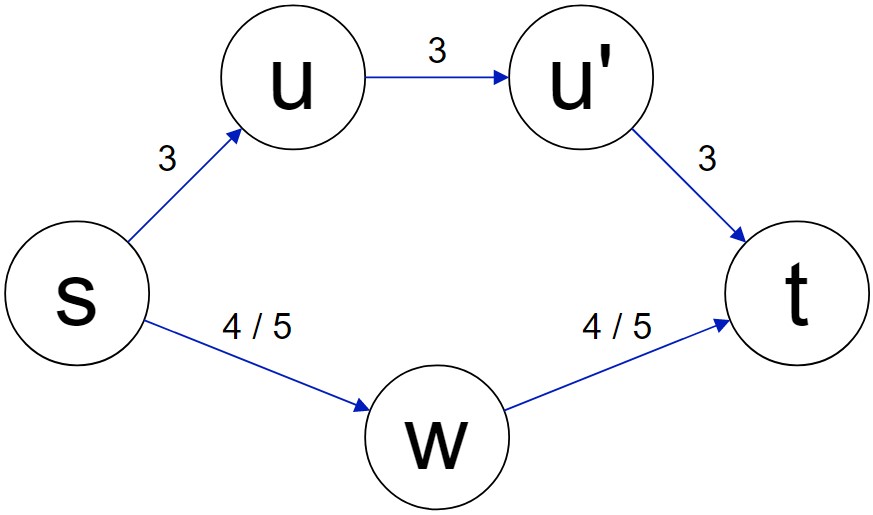
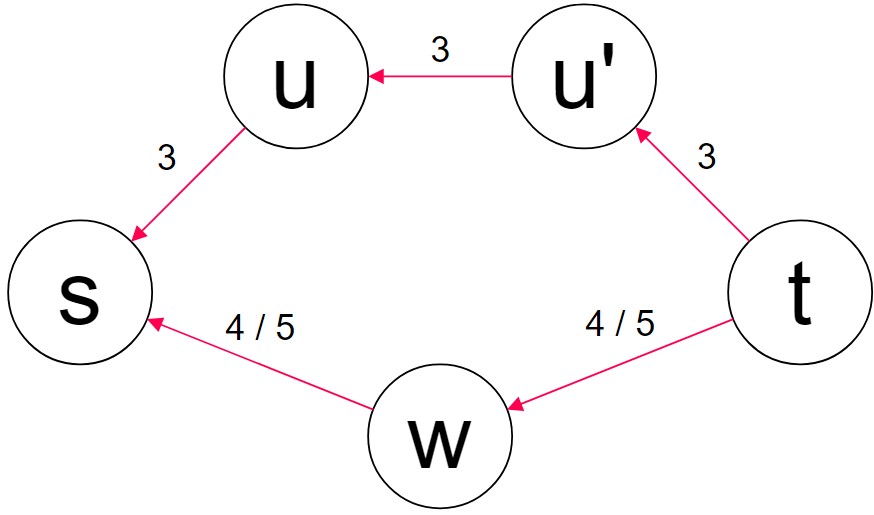
먼저 w 근처 간선의 가중치가 4인 그래프부터 양방향 다익스트라를 해보겠다. 다익스트라가 양방향으로 진행되는 것을 나타내기 위해 두 다익스트라의 결과를 /로 구분한다.
| S | s | u | u’ | w | t |
|---|---|---|---|---|---|
| {s} / {t} | 0 / ∞ | 3 / ∞ | ∞ / 3 | 4 / 4 | ∞ / 0 |
| {s, u} / {t, u’} | 0 / ∞ | 3 / 6 | 6 / 3 | 4 / 4 | ∞ / 0 |
| {s, u, u’} / {t, u’, u} | 0 / 9 | 3 / 6 | 6 / 3 | 4 / 4 | 9 / 0 |
| {s, u, u’, w} / {t, u’, u, w} | 0 / 8 | 3 / 6 | 6 / 3 | 4 / 4 | 8 / 0 |
| {s, u, u’, w, t} / {t, u’, u, w, s} | 0 / 8 | 3 / 6 | 6 / 3 | 4 / 4 | 8 / 0 |
다익스트라의 결과로 찾은 경로는 s > w > t이며, s에서 출발한 다익스트라와 t에서 출발한 다익스트라가 완전히 교차했을 때 완성되었다. s와 t가 처음 만난 시점인 u 또는 u'을 방문했을 때에는 경로는 만들어졌지만 최단 경로가 아닌 상태였다.
하고 싶은 말을 정리하자면, 양방향 다익스트라는 출발점과 도착점 둘이서 길을 찾는다는 장점이 있지만 두 탐색자가 완전히 교차해야만 최단경로를 확실히 알 수 있다는 것이다.
w 근처 간선의 가중치가 5인 그래프로 양방향 다익스트라를 하면 다음과 같다.
| S | s | u | u’ | w | t |
|---|---|---|---|---|---|
| {s} / {t} | 0 / ∞ | 3 / ∞ | ∞ / 3 | 5 / 5 | ∞ / 0 |
| {s, u} / {t, u’} | 0 / ∞ | 3 / 6 | 6 / 3 | 5 / 5 | ∞ / 0 |
| {s, u, u’} / {t, u’, u} | 0 / 9 | 3 / 6 | 6 / 3 | 5 / 5 | 9 / 0 |
| {s, u, u’, w} / {t, u’, u, w} | 0 / 9 | 3 / 6 | 6 / 3 | 5 / 5 | 9 / 0 |
| {s, u, u’, w, t} / {t, u’, u, w, s} | 0 / 9 | 3 / 6 | 6 / 3 | 5 / 5 | 9 / 0 |
이번에는 s와 t가 u와 u'을 방문했을 때 최단 경로가 완성되었다. 좋긴 한데, 위와 같은 반례가 있으니 교차할 때까지 탐색하는 게 맞다.
양방향 다익스트라 개선
문제: 이 양방향 검색 알고리즘을 개선할 수 있습니까? 절차를 설명하세요.
개선이라는 말은 현재의 양방향 다익스트라에 어딘가 비효율적인 부분이 있다는 뜻이다. 어디가 비효율적일까? 내가 보기엔 두 탐색자가 완전히 교차할 때까지 탐색을 진행해야만 하는 부분일 것 같다. 두 탐색자가 교차하지 않아도 최단경로를 찾을 방법이 있을까?
얄팍한 생각이지만 두 탐색자가 서로의 방문 기록을 공유해서, 이미 지나온 길은 가지 않게 하는 건 어떨까? 앞선 문제에서도 항상 가장 가까운 점으로 간다는 다익스트라의 특성 때문에 두 탐색자가 서로의 정점까지 방문한 후에, 다른 정점에 방문해서까지 최단경로를 찾을 수 있었다.
위의 문제로 예를 들자면, s와 t가 서로의 교차를 위해 각각 u'과 u를 방문해야 하긴 하지만 출발점과 도착점인 s와 t를 다시 방문할 필요는 없다. 그러니 각 탐색자에게 플래그를 주어서 한 번 방문 정점이 겹치면 플래그를 올리고, 플래그가 올라간 상태로 중복된 정점을 또 방문하려고 하면 유턴하게 만드는 거다. 두 탐색자의 경로를 합쳐야 하니까 방문 정점이 아예 안 겹칠 수는 없고, 한 번만 겹치게 하자는 말이다. 일단은 이 정도 생각이다.
